题目内容

【题目】（题类A）以椭圆 +y2=1（a＞1）短轴端点A（0，1）为直角顶点，作椭圆内接等腰直角三角形，试判断并推证能作出多少个符合条件的三角形．

【答案】解：设三角形另外两顶点为B，C，不妨设lAB：y=kx+1（k＞0），lAC：y=﹣ x+1．
由 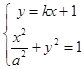，得（1+a2k2）x2+2ka2x=0，
∴|AB|= = ．
同理可得：|AC|= ．
由|AB|=|AC|得，k3﹣a2k2+a2k﹣1=0，
即（k﹣1）[k2+（1﹣a2）k+1]=0，解得k=1或k2+（1﹣a2）k+1=0．
对于k2+（1﹣a2）k+1=0，
由（1﹣a2）2﹣4=0，得a= ，此时方程的根k=1；
当1＜a＜ 时，方程k2+（1﹣a2）k+1=0无实根；
当a＞ 时，方程k2+（1﹣a2）k+1=0有两个不等实数根．
∴当a＞ 时，这样的三角形有3个；当1＜a≤ 时这样的三角形有1个．
【解析】由题意设出等腰直角三角形两边所在直线方程：lAB：y=kx+1（k＞0），lAC：y=﹣ x+1，分别联立直线方程和椭圆方程，求出|AB|，|AC|的长度，利用|AB|=|AC|得，k3﹣a2k2+a2k﹣1=0，然后分析方程根的情况得答案．

练习册系列答案
相关题目

【题目】已知a∈R，函数f（x）=x2﹣2ax+5．
（1）若a＞1，且函数f（x）的定义域和值域均为[1，a]，求实数a的值；
（2）若不等式x|f（x）﹣x2|≤1对x∈[ ， ]恒成立，求实数a的取值范围．

【题目】若y=f（x）=Asin（ωx+φ）（A＞0，ω＞0， 的部分图象如图所示．
（I）求函数y=f（x）的解析式；
（II）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象；若y=g（x）图象的一个对称中心为 ，求θ的最小值．

【题目】已知向量 ， 满足| |=| =1，且|k + |= | ﹣k |（k＞0），令f（k）= ． （Ⅰ）求f（k）= （用k表示）；
（Ⅱ）若f（k）≥x2﹣2tx﹣ 对任意k＞0，任意t∈[﹣1，1]恒成立，求实数x的取值范围．

【题目】已知指数函数y=g（x）满足g（3）=8，又定义域为实数集R的函数f（x）= 是奇函数．
（1）讨论函数y=f（x）的单调性；
（2）若对任意的t∈R，不等式f（2t﹣3t2）+f（t2﹣k）＞0恒成立，求实数k的取值范围．

【题目】已知函数f（x）=sin2 + sin cos ． （Ⅰ）求f（x）的最小正周期；
（Ⅱ）若x∈[ ，π]，求f（x）的最大值与最小值．

【题目】设数列{an}的前n项和Sn=2an﹣a1 ， 且a1 ， a2+1，a3成等差数列．
（1）求数列{an}的通项公式；
（2）记数列 的前n项和Tn ， 求使得 成立的n的最小值．

【题目】已知数列{an}中，a1=2，a2=3，an＞0，且满足an+12﹣an=an+1+an2（n∈N*）．
（1）求数列{an}的通项公式；
（2）设 ，求数列{bn}的前n项和Tn；
（3）设 （λ为正偶数，n∈N*），是否存在确定λ的值，使得对任意n∈N* ， 有Cn+1＞Cn恒成立，若存在，求出λ的值，若不存在，说明理由．

【题目】已知函数 （其中a为非零实数），且方程 有且仅有一个实数根． （Ⅰ）求实数a的值；
（Ⅱ）证明：函数f（x）在区间（0，+∞）上单调递减．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网