题目内容
如图,已知在侧棱垂直于底面三棱柱ABC—A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1.
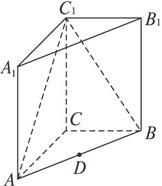
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1.

(1)证明:∵在△ABC中,AC="3,AB=5,BC=4,"
∴△ABC为直角三角形
.∴AC⊥CB.……………2分 又∵CC1⊥面ABC,AC 面ABC,
面ABC,
∴AC⊥CC1.……………4分
∴AC⊥面BCC1B1.又BC1 面BCC1B1,∴AC⊥BC1.……………6分
面BCC1B1,∴AC⊥BC1.……………6分
(2)证明:连接B1C交BC1于E,则E为BC1的中点,连接DE,
则在△ABC1中,DE∥AC1.……………8分 又DE 面CDB1……………9分
面CDB1……………9分
AC1 面CDB1………10分 则AC1∥面B1CD……………12分
面CDB1………10分 则AC1∥面B1CD……………12分
∴△ABC为直角三角形
.∴AC⊥CB.……………2分 又∵CC1⊥面ABC,AC
 面ABC,
面ABC,∴AC⊥CC1.……………4分
∴AC⊥面BCC1B1.又BC1
 面BCC1B1,∴AC⊥BC1.……………6分
面BCC1B1,∴AC⊥BC1.……………6分(2)证明:连接B1C交BC1于E,则E为BC1的中点,连接DE,
则在△ABC1中,DE∥AC1.……………8分 又DE
 面CDB1……………9分
面CDB1……………9分AC1
 面CDB1………10分 则AC1∥面B1CD……………12分
面CDB1………10分 则AC1∥面B1CD……………12分略

练习册系列答案
相关题目
 中,
中, 是
是 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且 .
. ;
; 平面
平面 ,求
,求 的值.[
的值.[
 ,
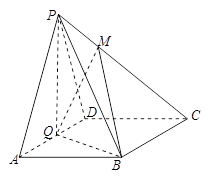
, ,
, 中,若
中,若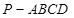 中,底面
中,底面 为菱形,
为菱形,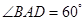 ,
,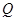 为
为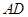 的中点,
的中点,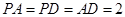 .
.
 平面
平面 ;
;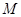 在线段
在线段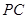 上,
上,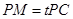 ,试确定
,试确定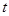 的值,使
的值,使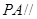 平面
平面 ;
;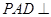 平面
平面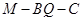 的大小.
的大小.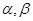 是不重合的平面,则下列条件中可推出a∥b的是( )
是不重合的平面,则下列条件中可推出a∥b的是( )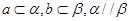 ?
?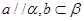
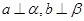 ?
?
 ABC=60
ABC=60 ,E
,E C
C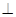 面ABCD,FA
面ABCD,FA
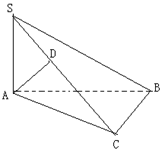
 中,四边形
中,四边形 为平行四边形,且面
为平行四边形,且面 面
面 ,
, ,且
,且 ,
, 为
为 中点.
中点. 平面
平面 与平面
与平面 所成角的正弦值.
所成角的正弦值.
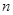
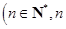 ≥
≥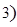 条直线,其中任何两条不平行,任何三条不过同一点,若这
条直线,其中任何两条不平行,任何三条不过同一点,若这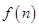 个平面区域,则
个平面区域,则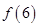 等于( )
等于( )