题目内容
(本小题10分)已知在三棱锥S--ABC中,∠ACB=900,又SA⊥平面ABC,
AD⊥SC于D,求证:AD⊥平面SBC,
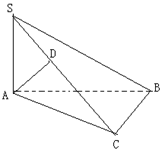
AD⊥SC于D,求证:AD⊥平面SBC,

证明:SA⊥面ABC, BC⊥面ABC,Þ BC ⊥SA;
又BC⊥AC,且AC、SA是面SAC内的两相交线,∴BC⊥面SAC;
又ADÌ面SAC,∴ BC⊥AD,
又已知SC⊥AD,且BC、SC是面SBC内两相交线,∴ AD⊥面SBC。
又BC⊥AC,且AC、SA是面SAC内的两相交线,∴BC⊥面SAC;
又ADÌ面SAC,∴ BC⊥AD,
又已知SC⊥AD,且BC、SC是面SBC内两相交线,∴ AD⊥面SBC。
略

练习册系列答案
相关题目
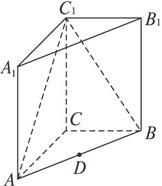
 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
, .
.
 中,底面
中,底面 是菱形,
是菱形, .
. ,求证:
,求证: 平面
平面 ;
; 平
平 面
面 ;
; 上是否存在点
上是否存在点 (异于点
(异于点 )使得
)使得 ∥平面
∥平面 ,若存在,求
,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 中,底面
中,底面 是
是 的菱形,
的菱形, ,
, ,点
,点 在棱
在棱 上,点
上,点 是棱
是棱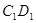 的中点;
的中点; ;
; 的长度,使得
的长度,使得 为直二面角。
为直二面角。
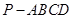 中,底面
中,底面 为正方形,侧棱
为正方形,侧棱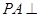 底面
底面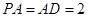 ,点
,点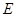 为
为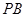 的中点。
的中点。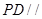 平面
平面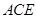 ;
;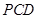 的距离。
的距离。

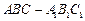 中,
中,  底面
底面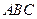 ,
,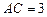 ,
, 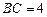 ,
,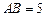 , 点D是
, 点D是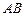 的中点.
的中点.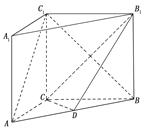
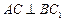 ; (Ⅱ) 求证
; (Ⅱ) 求证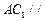 ∥平面
∥平面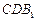 .
.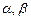 为两个不重合的平面,
为两个不重合的平面,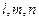 为两两不重合的直线,给出下列四个命题:①若
为两两不重合的直线,给出下列四个命题:①若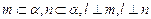 ,则
,则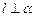 ;②若
;②若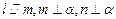 ,则
,则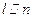 ;③若
;③若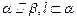 ,则
,则 ;④若
;④若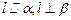 ,则
,则 .其中正确命题的序号是 ▲ .
.其中正确命题的序号是 ▲ .