题目内容
9.已知x,y∈(-$\sqrt{3}$,$\sqrt{3}$)且xy=-1,则s=$\frac{3}{3-{x}^{2}}$+$\frac{12}{12-{y}^{2}}$的最小值为$\frac{12}{5}$.分析 先将关于s的表达式整理,再根据xy=1,得到s=1+$\frac{35}{37-1{2x}^{2}-{3y}^{2}}$,由基本不等式的性质求出即可.
解答 解:s=$\frac{3}{3-{x}^{2}}$+$\frac{12}{12-{y}^{2}}$
=$\frac{3(12{-y}^{2})+12(3{-x}^{2})}{(3{-x}^{2})(12{-y}^{2})}$
=$\frac{72-1{2x}^{2}-{3y}^{2}}{36-1{2x}^{2}-{3y}^{2}{{+x}^{2}y}^{2}}$,
∵xy=-1,∴x2y2=1,
∴s=$\frac{72-1{2x}^{2}-{3y}^{2}}{37-1{2x}^{2}-{3y}^{2}}$
=1+$\frac{35}{37-1{2x}^{2}-{3y}^{2}}$,
∵12x2+3y2≥2$\sqrt{3{{6x}^{2}y}^{2}}$=12,
∴s≥1+$\frac{35}{37-12}$=$\frac{12}{5}$,
当且仅当“12x2=3y2”即x=-$\frac{\sqrt{2}}{2}$,y=$\sqrt{2}$或x=$\frac{\sqrt{2}}{2}$,y=-$\sqrt{2}$时“=”成立,
故答案为:$\frac{12}{5}$.
点评 本题考查了函数的最值问题,考查基本不等式的性质,是一道中档题.

练习册系列答案
相关题目
19.计算$\frac{5}{i-2}$(i为虚数单位)的值是( )
| A. | i+2 | B. | i-2 | C. | -2-i | D. | 2-i |
20.已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x>1),则最大角为( )
| A. | 150° | B. | 120° | C. | 60° | D. | 75° |
1.下列说法正确的是( )
| A. | 命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0或y≠0” | |
| B. | 若命题p为假命题,命题¬q为真命题,则命题“p∨q”为真命题 | |
| C. | “$\frac{a}{b}$>1”是“a>b>0”的必要不充分条件 | |
| D. | 命题“任意x>1,x+1>2”的否定是“存在x≤1,x+1≤2” |
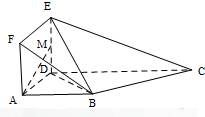 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.