题目内容
4.已知函数f(x)=x2+bx+2,g(x)=|x2-1|,x∈R.(1)若函数f(x)满足f(x+3)=f(-x),求实数b的值;
(2)在(1)的条件下,求使不等式g(x)≤f(x)成立的x的取值集合;
(3)若函数h(x)=f(x)+g(x)+2在(0,2)上有两个不同的零点x1,x2,求实数b的取值范围.
分析 (1)根据f(3+x)=f(-x),可得二次函数的对称轴为x=$\frac{3}{2}$,即可求得b的值;
(2)代入f(x),将g(x)分类讨论去掉绝对值,再分类讨论,根据不同的解析式列出不等式求解,即可得到答案;
(3)将h(x)的解析式表示出来,分b=0和b≠0分类研究,当b=0时,不合题意,当b≠0时,根据h(x)的单调性,确定ϕ(x)在(0,1)上至多一个零点,不妨设0<x1<x2<2,对0<x1<1,1≤x2<2时,及1≤x1<x2<2时分别进行求解,即可得到实数b的取值范围.
解答 解:(1)∵f(3+x)=f(-x)
∴函数f (x)的图象关于直线x=$\frac{3}{2}$对称,
∵f(x)=x2+bx+2,
∴-$\frac{b}{2}$=$\frac{3}{2}$,解得b=-3,
(2)f(x)=x2-3x+2,g(x)=|x2-1|=$\left\{\begin{array}{l}{{x}^{2}-1,x≤-1或x≥1}\\{1-{x}^{2},-1<x<1}\end{array}\right.$,
①当x≤-1,或x≥1时,
∵f(x)≥g(x),
∴x2-3x+2≥x2-1,解得x≤1,
∴此时x的范围为x≤-1,或x=1;
②当-1<x<1时,
∵f(x)≥g(x),
∴x2-3x+2≥1-x2,解得x≤$\frac{1}{2}$或x≥1,
∴此时x的范围为-1<x≤$\frac{1}{2}$.
∴综合①②可得,使不等式f(x)≥g(x)成立的x的取值集合为{x|x≤$\frac{1}{2}$或x=1}.
(3)∵h(x)=f(x)+g(x)+2,且f(x)=x2+bx+2,g(x)$\left\{\begin{array}{l}{{x}^{2}-1,x≤-1或x≥1}\\{1-{x}^{2},-1<x<1}\end{array}\right.$,
∴h(x)=$\left\{\begin{array}{l}{2{x}^{2}+bx+3,x≤-1或x≥1}\\{bx+5,-1<x<1}\end{array}\right.$,
若b=0时,h(x)=$\left\{\begin{array}{l}{2{x}^{2}+3,x≤-1或x≥1}\\{5,-1<x<1}\end{array}\right.$,显然h(x)>0恒成立,不满足条件;
若b≠0时,函数ϕ(x)=bx+5在(0,1)上是单调函数,即ϕ(x)在(0,1)上至多一个零点,不妨设0<x1<x2<2,
①当0<x1<1,1≤x2<2时,则ϕ(0)ϕ(1)<0,且h(1)h(2)≤0,
∴$\left\{\begin{array}{l}{b+5<0}\\{(b+5)(2b+11)≤0}\end{array}\right.$,解得-$\frac{11}{2}$≤b<-5;
经检验b=-$\frac{11}{2}$时,h(x)的零点为$\frac{10}{11}$,2(舍去),
∴-$\frac{11}{2}$<b<-5.
②当1≤x1<x2<2时,
∵ϕ(x)在(0,1)上至多一个零点,
∴$\left\{\begin{array}{l}{b+5≥0}\\{2b+11>0}\\{-8<b<-4}\\{b<-2\sqrt{6}或b>2\sqrt{6}}\end{array}\right.$,解得-5≤b<-2$\sqrt{6}$.
∴综上所述,b的取值范围为-$\frac{11}{2}$<b<-2$\sqrt{6}$.
点评 本题考查了二次函数的性质,对于二次函数要注意数形结合的应用,注意抓住二次函数的开口方向,对称轴,以及判别式的考虑.考查了函数的零点与方程根的关系.函数的零点等价于对应方程的根,等价于函数的图象与x轴交点的横坐标,解题时要注意根据题意合理的选择转化.属于中档题.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | S△ABC2=S△BOC•S△BDC | B. | S△ABD2=S△BOD•S△BDC | ||
| C. | S△ADC2=S△DOC•S△BDC | D. | S△DBC2=S△ABD•S△ABC |
| A. | -$\frac{2}{3}$ | B. | -$\frac{\sqrt{5}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
| A. | 2 | B. | 6 | C. | -2 | D. | 1 |
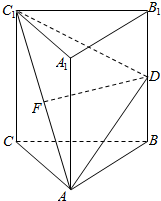 如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.
如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.