题目内容
14.数列{an}满足a1=1,前n项和为Sn,Sn+1=4an+2,求a2013.分析 化简可得an+1-2an=2(an-2an-1),从而可得数列{an+1-2an}是以3为首项,以2为公比的等比数列,即an+1-2an=3•2n-1,从而可得数列{$\frac{{a}_{n}}{{2}^{n}}$}是以$\frac{1}{2}$为首项,以$\frac{3}{4}$为公差的等差数列,从而解得.
解答 解:∵Sn+1=4an+2,
∴a1+a2=4a1+2,
解得,a2=5;
由Sn=4an-1+2,Sn+1=4an+2得,
an+1=4an-4an-1,
an+1-2an=2(an-2an-1),
故数列{an+1-2an}是以3为首项,以2为公比的等比数列,
∴an+1-2an=3•2n-1,
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{3}{4}$,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}是以$\frac{1}{2}$为首项,以$\frac{3}{4}$为公差的等差数列,
∴$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}$+$\frac{3}{4}$(n-1)=$\frac{3}{4}$n-$\frac{1}{4}$,
∴an=($\frac{3}{4}$n-$\frac{1}{4}$)2n,
∴a2013=($\frac{3}{4}$×2013-$\frac{1}{4}$)22013=3019×22012.
点评 本题考查了等差数列与等比数列的应用及数列的化简与构造,属于难题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
4.若函数f(x)=x2-2x,x∈[-2,4],则f(x)的值域为( )
| A. | [-1,8] | B. | [-1,16] | C. | [-2,8] | D. | [-2,4] |
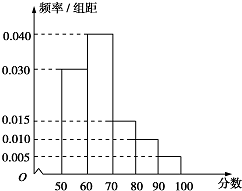 某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.
某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.