题目内容
18.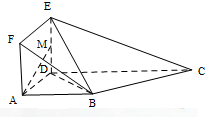 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.(1)若M为ED的中点,求证:AM∥平面BEC;
(2)求证:BC⊥BM.
分析 (1)若M为ED的中点,取CD的中点H,根据面面平行的性质定理即可证明AM∥平面BEC;
(2)根据线面垂直的性质定理证明BC⊥平面BDE即可证明BC⊥BM.
解答  证明:(1)若M为ED的中点,取CD的中点H,连接MH,AH,
证明:(1)若M为ED的中点,取CD的中点H,连接MH,AH,
则MH是△CDE的中位线,
∴MH∥CE,
∵MH?平面BEC,CE?平面BEC,
∴MH∥平面BEC
在梯形ABCD中,∵AB=AD=$\frac{1}{2}$CD=1,
∴CH=AB,
即四边形ABCH为平行四边形,
∴AH∥BC,
∵AH?平面BEC,BC?平面BEC,
∴AH∥平面BEC
∵AH∩MH=H,
∴平面AMH∥平面BEC,
∵AM?平面AMH,
∴AM∥平面BEC;
(2)∵AB=AD=$\frac{1}{2}$CD=1,H是CD的中点,
∴BD⊥BC,
∵平面ADEF⊥平面ABCD,ADEF为正方形
∴ED⊥平面ABCD,ED⊥BC,
∵BD∩ED=D,
∴BC⊥平面BDE,
∵BM?平面BDE,
∴BC⊥BM.
点评 本题主要考查线面平行和垂直的判定,根据相应的判定定理以及性质定理是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.
某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.