题目内容
【题目】已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|:|MN|=________.
【答案】![]()
【解析】分析:求出抛物线C的焦点F的坐标,从而得到AF的斜率k=![]() .过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|.Rt△MPN中,根据tan∠MNP=
.过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|.Rt△MPN中,根据tan∠MNP=![]() ,从而得到|PN|=2|PM|,进而算出|MN|=
,从而得到|PN|=2|PM|,进而算出|MN|=![]() |PM|,由此即可得到|FM|:|MN|的值.
|PM|,由此即可得到|FM|:|MN|的值.
详解::∵抛物线C:x2=4y的焦点为F(0,1),点A坐标为(2,0)
∴抛物线的准线方程为l:y=-1,直线AF的斜率为k=![]() ,过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|∵Rt△MPN中,tan∠MNP=-k=
,过M作MP⊥l于P,根据抛物线物定义得|FM|=|PM|∵Rt△MPN中,tan∠MNP=-k=![]() ,∴|PN|=2|PM|,
,∴|PN|=2|PM|,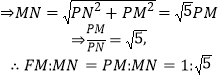
故答案为![]()

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
