题目内容
设p:2∈{x||x-a|>1};q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点,如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
∵2∈{x||x-a|>1},
∴|2-a|>1⇒a>3或a<1,
∴命题p为真时:a>3或a<1;
∵曲线y=x2+(2a-3)x+1与x轴交于不同的两点,则△>0⇒a<
或a>
,
∴命题q为真时:a<
或a>
,
由复合命题真值表得:p∨q为真命题,p∧q为假命题,则命题p、q一真一假,
当p真q假时,
≤a<1;
当p假q真时,
<a≤3
综上实数a的取值范围是
<a≤3或
≤a<1.
∴|2-a|>1⇒a>3或a<1,
∴命题p为真时:a>3或a<1;
∵曲线y=x2+(2a-3)x+1与x轴交于不同的两点,则△>0⇒a<
| 1 |
| 2 |
| 5 |
| 2 |
∴命题q为真时:a<
| 1 |
| 2 |
| 5 |
| 2 |
由复合命题真值表得:p∨q为真命题,p∧q为假命题,则命题p、q一真一假,
当p真q假时,
| 1 |
| 2 |
当p假q真时,
| 5 |
| 2 |
综上实数a的取值范围是
| 5 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
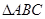 中,角
中,角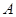 、
、 、
、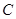 所对应的变分别为
所对应的变分别为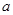 、
、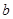 、
、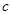 ,则
,则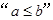 是
是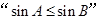 的( )
的( )