题目内容
已知P:实数x满足x2-2x-3<0;Q:实数x满足
<0.
(Ⅰ)在区间(-5,4)上任取一个实数x,求事件“P∨Q为真命题”发生的概率;
(Ⅱ)若数对(m,n)中,m∈{x∈Z|x满足P},n∈{x∈Z|x满足Q},求事件“n-m∈{x|x满足‘P∧Q'}”发生的概率.
| x-2 |
| x+3 |
(Ⅰ)在区间(-5,4)上任取一个实数x,求事件“P∨Q为真命题”发生的概率;
(Ⅱ)若数对(m,n)中,m∈{x∈Z|x满足P},n∈{x∈Z|x满足Q},求事件“n-m∈{x|x满足‘P∧Q'}”发生的概率.
(Ⅰ)P为真命题?x2-2x-3<0,x∈R?-1<x<3;
Q为真命题?
<0,x∈R?(x-2)(x+3)<0,x∈R?-3<x<2;
又P∨Q为真命题,
∴P为真命题或Q为真命题,即-3<x<3,
∴区间(-5,4)的长度为9,区间(-3,3)的长度为6,
由几何概型知p1=
=
故在区间(-5,4)上任取一个实数x,
事件“P∨Q为真命题”发生的概率为
.
(Ⅱ)由(Ⅰ)知,m=0、1、2,n=-2、-1、0、1,
则基本事件(m,n)共有12个:(0,-2),(0,-1),(0,0),(0,1),(1,-2),(1,-1),
(1,0),(1,1),(2,-2),(2,-1),(2,0),(2,1).
又“x满足P∧Q”?
?-1<x<2,
∴符合“n-m∈{x|x满足‘P∧Q'}”的基本事件共有3个:(0,0),(0,1),(1,1).
由古典概型知p2=
=
故事件“n-m∈{x|x满足‘P∧Q'}”的发生概率为
.
Q为真命题?
| x-2 |
| x+3 |
又P∨Q为真命题,
∴P为真命题或Q为真命题,即-3<x<3,
∴区间(-5,4)的长度为9,区间(-3,3)的长度为6,
由几何概型知p1=
| 6 |
| 9 |
| 2 |
| 3 |
故在区间(-5,4)上任取一个实数x,
事件“P∨Q为真命题”发生的概率为
| 2 |
| 3 |
(Ⅱ)由(Ⅰ)知,m=0、1、2,n=-2、-1、0、1,
则基本事件(m,n)共有12个:(0,-2),(0,-1),(0,0),(0,1),(1,-2),(1,-1),
(1,0),(1,1),(2,-2),(2,-1),(2,0),(2,1).
又“x满足P∧Q”?
|
∴符合“n-m∈{x|x满足‘P∧Q'}”的基本事件共有3个:(0,0),(0,1),(1,1).
由古典概型知p2=
| 3 |
| 12 |
| 1 |
| 4 |
故事件“n-m∈{x|x满足‘P∧Q'}”的发生概率为
| 1 |
| 4 |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
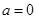 ”是复数
”是复数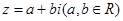 为纯虚数的 条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
为纯虚数的 条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)