题目内容
若a，b，c∈R，且|a-c|＜|b|，则正确的是（ ）
| A．|a|＜|b|+|c| | B．|a|＜|b|-|c| | C．|a|＞|b|+|c| | D．|a|＞|b|-|c| |
由|a-c|＜|b|，得当a=b=2，c=1时，B、C两项的不等式均不成立；
当a=c=0，b=1时，D项中的不等式不成立．
因此，只有A项中的不等式正确，证明如下：
∵|a|-|c|≤|a-c|，
∴由题意|a-c|＜|b|，可得|a|-|c|＜|b|，
移项得|a|＜|b|+|c|，不等式成立．
故选：A
当a=c=0，b=1时，D项中的不等式不成立．
因此，只有A项中的不等式正确，证明如下：
∵|a|-|c|≤|a-c|，
∴由题意|a-c|＜|b|，可得|a|-|c|＜|b|，
移项得|a|＜|b|+|c|，不等式成立．
故选：A
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
的解集为 .
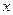的不等式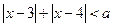
的解集不是空集，求参数
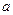的取值范围。
的解集为 . 
。