题目内容
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?
(1)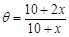 ;(2)参考解析
;(2)参考解析
解析试题分析:(1)由于花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.所以AD的弧长为
弧度.所以AD的弧长为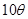 ,BC的弧长为
,BC的弧长为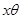 .所以可得
.所以可得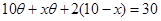 .即可得结论.
.即可得结论.
(2)由花坛两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.即可得所需费用的关系式. 花坛的面积由大扇形面积减去小的扇形面积即可,再利用基本不等式即可求得结论.
试题解析:(1)设扇环的圆心角为q,则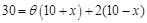 ,
,
所以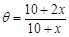 ,
,
(2)花坛的面积为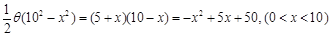 .
.
装饰总费用为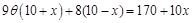 ,
,
所以花坛的面积与装饰总费用的比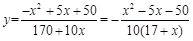 ,
,
令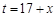 ,则
,则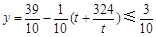 ,当且仅当t=18时取等号,
,当且仅当t=18时取等号,
此时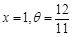 .
.
答:当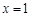 时,花坛的面积与装饰总费用的比最大.
时,花坛的面积与装饰总费用的比最大.
考点:1.扇形的面积.2.函数的最值.3.基本不等式的应用.

练习册系列答案
相关题目
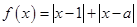 .
. 时,解不等式
时,解不等式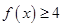 ;
;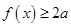 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.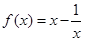 .
. 的奇偶性,并加以证明;
的奇偶性,并加以证明; 上为增函数;
上为增函数;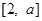 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于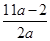 ,求
,求 的取值范围.
的取值范围. (
(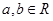 ),其图像在
),其图像在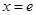 处的切线方程为
处的切线方程为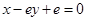 .函数
.函数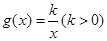 ,
, .
.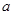 、
、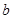 的值;
的值;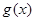 图像上一点为圆心,2为半径作圆
图像上一点为圆心,2为半径作圆 ,若圆
,若圆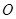 的距离为1,求
的距离为1,求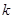 的取值范围;
的取值范围;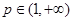 ,存在实数
,存在实数 、
、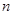 满足
满足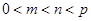 ,使得
,使得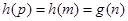 .
.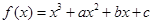 在
在 与
与 时都取得极值.
时都取得极值. 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.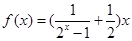 .
. 的奇偶性;(3)求证:
的奇偶性;(3)求证: 的焦点为
的焦点为 ,点
,点 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
. 是抛物线上的两点,
是抛物线上的两点,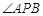 的角平分线与
的角平分线与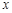 轴垂直,求
轴垂直,求 的面积最大时直线
的面积最大时直线 的方程.
的方程.