题目内容
已知函数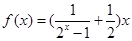 .
.
(1)求函数的定义域;(2)判断函数 的奇偶性;(3)求证:
的奇偶性;(3)求证: ﹥0.
﹥0.
(1)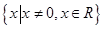 ;(2)偶函数,证明见解析;(3)证明见解析.
;(2)偶函数,证明见解析;(3)证明见解析.
解析试题分析:(1)由分母 不能为零得求解即可;(2)在(1)的基础上,只要再判断
不能为零得求解即可;(2)在(1)的基础上,只要再判断 与
与 的关系即可;(3)在(2)的基础上要证明对称区间上成立可即可.不妨证明:当
的关系即可;(3)在(2)的基础上要证明对称区间上成立可即可.不妨证明:当 时,则有
时,则有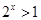 进而有
进而有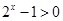 ,
, ,然后得到
,然后得到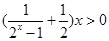 ,再由奇偶性得到对称区间上的结论.
,再由奇偶性得到对称区间上的结论.
试题解析:(1)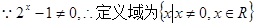 .
.
(2)设
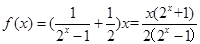 ,
, ,
, 为偶函数.
为偶函数.
(3)当 时,
时, <
< <1,
<1, -1<
-1< <0,
<0, <
< .
.
又 ,则
,则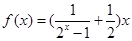 >0,
>0,
由 为偶函数知,当x>0时,
为偶函数知,当x>0时, >0,
>0,
综上可知当 >0.
>0.
考点:1、函数的定义域及其求法;2、函数的值域;3、函数奇偶性的判断.

练习册系列答案
相关题目
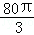 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
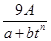 ,其中
,其中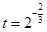 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.  为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当 的定义域为E,值域为F.
的定义域为E,值域为F.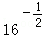 与集合F的关系;
与集合F的关系;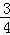 },求实数a的值.
},求实数a的值.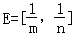 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值. ,
, .
. 的最小正周期和值域;
的最小正周期和值域; ,且
,且 ,求
,求 的值.
的值.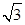 sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为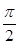 .
.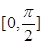 ,求点A的坐标.
,求点A的坐标. 的图象分别与
的图象分别与 轴相交于两点
轴相交于两点 ,且向量
,且向量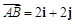 (
( 分别是与
分别是与 .
. 的值;
的值; 的解集为
的解集为 ,求
,求 的值
的值