题目内容
已知函数 (
(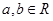 ),其图像在
),其图像在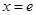 处的切线方程为
处的切线方程为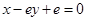 .函数
.函数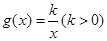 ,
, .
.
(1)求实数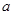 、
、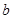 的值;
的值;
(2)以函数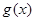 图像上一点为圆心,2为半径作圆
图像上一点为圆心,2为半径作圆 ,若圆
,若圆 上存在两个不同的点到原点
上存在两个不同的点到原点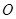 的距离为1,求
的距离为1,求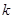 的取值范围;
的取值范围;
(3)求最大的正整数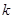 ,对于任意的
,对于任意的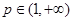 ,存在实数
,存在实数 、
、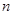 满足
满足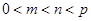 ,使得
,使得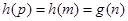 .
.
(1) ;(2)
;(2)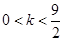 ;(3)
;(3) .
.
解析试题分析:(1)由已知可先求出切点坐标和斜率,又切点在函数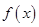 图象上,且在该处的导数等于切线的斜率,从而可列方程组为
图象上,且在该处的导数等于切线的斜率,从而可列方程组为 ,故可求出实数
,故可求出实数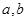 的值;(2)根据题意可将问题转化为圆
的值;(2)根据题意可将问题转化为圆 与以原点
与以原点 为圆心、1为半径的圆
为圆心、1为半径的圆 有两个不同交点,即两圆相交,考虑到两圆的半径差为1、和为3,所以两圆心距离的范围应为
有两个不同交点,即两圆相交,考虑到两圆的半径差为1、和为3,所以两圆心距离的范围应为 ,再通过配方法,从而可求出实数
,再通过配方法,从而可求出实数 的取值范围;(3)考虑到函数
的取值范围;(3)考虑到函数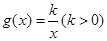 在区间
在区间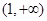 上为减函数,又
上为减函数,又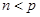 ,所以
,所以 ,若
,若 ,则对任意
,则对任意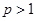 ,有
,有 ,即当
,即当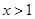 时,要有
时,要有 ,整理有
,整理有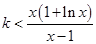 ,令
,令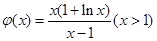 ,由函数的单调性、最值及零点可得
,由函数的单调性、最值及零点可得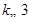 ,从而问题可得证,这题有一定难度.
,从而问题可得证,这题有一定难度.
试题解析:(1) 当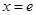 时,
时, ,
,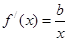 ,故
,故 ,解得
,解得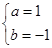 . 3分
. 3分
(2)问题即为圆 与以
与以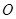 为圆心1为半径的圆有两个交点,即两圆相交.设
为圆心1为半径的圆有两个交点,即两圆相交.设 ,则
,则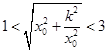 ,即
,即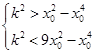 ,
,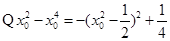 ,
,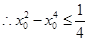 ,
,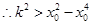 必定有解; 6分
必定有解; 6分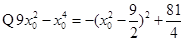 ,
,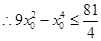 ,
,
故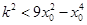 有解,须
有解,须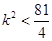 ,又
,又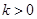 ,从而
,从而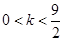 . 8分
. 8分
(3)显然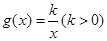 在区间
在区间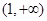 上为减函数,于是
上为减函数,于是 ,若
,若 ,则对任意
,则对任意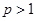 ,有
,有 .
.
当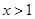 时,
时,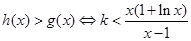 ,令
,令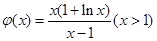 ,
,
则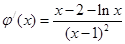 .令
.令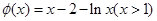 ,则
,则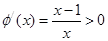 ,故
,故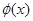 在
在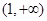 上为增函数,又
上为增函数,又 ,
, ,因此存在唯一正实数
,因此存在唯一正实数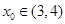 ,使
,使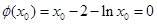 .故当
.故当 时,
时,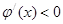 ,
,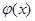 为减函数;当
为减函数;当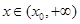 时,
时, ,
,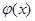 为增函数,因此
为增函数,因此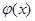 在
在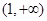 有最小值
有最小值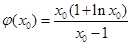 ,又
,又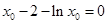 ,化简得
,化简得

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
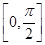 上恒成立.
上恒成立.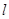 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.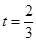 时,求直路
时,求直路
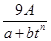 ,其中
,其中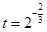 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍. 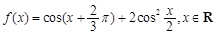 .
. 的值域;
的值域;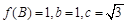 ,求a的值.
,求a的值. 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当 的定义域为E,值域为F.
的定义域为E,值域为F. 与集合F的关系;
与集合F的关系; },求实数a的值.
},求实数a的值.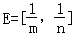 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.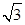 sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为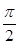 .
.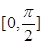 ,求点A的坐标.
,求点A的坐标. 时,f
时,f >f
>f ;
; <0.
<0.