题目内容
已知抛物线 的焦点为
的焦点为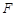 ,点
,点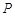 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,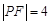 .
.
(1)求抛物线的方程;
(2)设点 是抛物线上的两点,
是抛物线上的两点, 的角平分线与
的角平分线与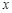 轴垂直,求
轴垂直,求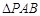 的面积最大时直线
的面积最大时直线 的方程.
的方程.
(1) ;(2)
;(2)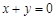
解析试题分析:(1)由于点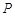 是抛物线上的一点,且其纵坐标为4,假设点
是抛物线上的一点,且其纵坐标为4,假设点 ,再通过
,再通过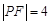 ,可得一个关于
,可得一个关于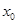 与
与 的关系式,在结合抛物线方程即可求出
的关系式,在结合抛物线方程即可求出 .从而求得抛物线的方程.
.从而求得抛物线的方程.
(2)因为 的角平分线与
的角平分线与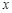 轴垂直,所以可知
轴垂直,所以可知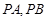 的倾斜角互补,即
的倾斜角互补,即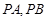 的斜率互为相反数.所以假设直线PA,联立抛物线方程即可得到点A的坐标,类比地求出点B的坐标.结合韦达定理,可以得到直线AB的斜率为定值-1.通过假设直线AB的方程,联立抛物线的方程,应用点到直线的距离,即可表示三角形的面积.再通过求最值即能到结论.
的斜率互为相反数.所以假设直线PA,联立抛物线方程即可得到点A的坐标,类比地求出点B的坐标.结合韦达定理,可以得到直线AB的斜率为定值-1.通过假设直线AB的方程,联立抛物线的方程,应用点到直线的距离,即可表示三角形的面积.再通过求最值即能到结论.
试题解析:(1)设 ,因为
,因为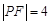 ,由抛物线的定义得
,由抛物线的定义得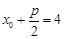 ,又
,又 ,所以
,所以 ,
,
因此 ,解得
,解得 ,从而抛物线的方程为
,从而抛物线的方程为 .
.
(2)由(1)知点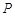 的坐标为
的坐标为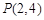 ,因为
,因为 的角平分线与
的角平分线与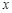 轴垂直,所以可知
轴垂直,所以可知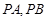 的倾斜角互补,即
的倾斜角互补,即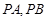 的斜率互为相反数
的斜率互为相反数
设直线 的斜率为
的斜率为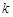 ,则
,则 ,由题意
,由题意 ,
,
把 代入抛物线方程得
代入抛物线方程得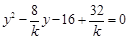 ,该方程的解为4、
,该方程的解为4、 ,
,
由韦达定理得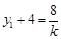 ,即
,即 ,同理
,同理 ,
,
所以 ,
,
设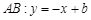 ,把
,把 代入抛物线方程得
代入抛物线方程得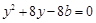 ,
,
由题意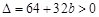 ,且
,且 ,从而
,从而
又 ,所以
,所以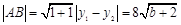 ,点
,点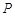 到
到 的距离
的距离 ,
,
因此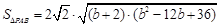 ,设
,设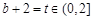 ,
,
则 ,
,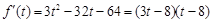
由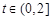 知
知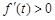 ,所以
,所以 在
在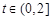 上为增函数,因此
上为增函数,因此 ,
,
即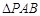 面积的最大值为
面积的最大值为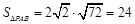 .
.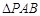 的面积取最大值时
的面积取最大值时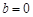 ,所以直线
,所以直线 的方程为
的方程为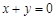 .
.
考点:1.抛物线的性质.2.函数的最值.3.等价变换.4.圆锥曲线与函数知识的交汇.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 为圆心的两个同心圆弧
为圆心的两个同心圆弧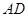 、弧
、弧 以及两条线段
以及两条线段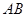 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.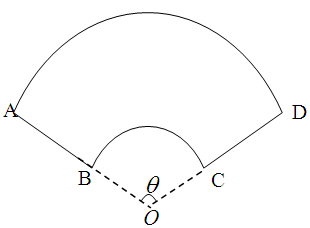
 ,当
,当 ,
, .
.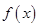 的最小正周期和值域;
的最小正周期和值域; ,且
,且 ,求
,求 的值.
的值. sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为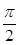 .
. ,求点A的坐标.
,求点A的坐标.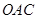 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域 内,乙中转站建在区域
内,乙中转站建在区域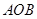 内.分界线
内.分界线 固定,且
固定,且 百米,边界线
百米,边界线 始终过点
始终过点 ,边界线
,边界线 满足
满足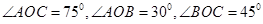 .
. (
(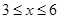 )百米,
)百米,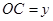 百米.
百米.
 表示成
表示成 的函数,并求出函数
的函数,并求出函数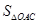 最小,并求出其面积的最小值.
最小,并求出其面积的最小值. 的图象分别与
的图象分别与 轴相交于两点
轴相交于两点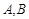 ,且向量
,且向量 (
( 分别是与
分别是与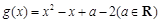 .
. 的值;
的值; 的解集为
的解集为 ,求
,求 的值
的值