Question

【题目】如图，正四棱锥中， 是正方形， 是正方形的中心， 底面， 是的中点．

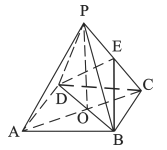
(I)证明： 平面；

(II)证明：平面平面；

(III)已知： ，求点到面的距离．

Answer 1

【答案】(Ⅰ)证明见解析；(Ⅱ)证明见解析；(Ⅲ)1.

【解析】试题分析：

(Ⅰ)连结EO，由三角形中位线的性质可知OE∥AP，利用线面平行的判定定理可得PA∥平面BDE.

(Ⅱ)利用线面垂直的判定定理可得POBD，利用正方形的性质可得ACBD，结合线面垂直的判定定理可得BD平面PAC，则平面PAC平面BDE.

(Ⅲ)设点C到面BDE的距离为,由三棱锥的性质可得，结合棱锥的体积公式可得关于高的方程，解方程可得点C到面BDE的距离为1.

试题解析：

（I）连结EO，在△BDE中∵O是AC的中点，E是PC的中点，

∴OE∥AP，又∵OE平面BDE，PA平面BDE，

∴PA∥平面BDE.

（II）∵PO底面ABCD，BD面ABCD,

∴POBD，

又∵ABCD是正方形， ∴ACBD， 且ACPO=O

∴BD平面PAC，

而BD平面BDE，∴平面PAC平面BDE.

（III）设点C到面BDE的距离为,

由已知得

正四棱锥P-ABCD中，AB=PA=2 ,由题意得，PO=,EO= =1,

∴，

∴=1，即点C到面BDE的距离为1