Question

【题目】已知定义域为的函数是奇函数

（Ⅰ）求值；

（Ⅱ）判断并证明该函数在定义域上的单调性；

（Ⅲ）若对任意的，不等式恒成立，求实数的取值范围；

（Ⅳ）设关于的函数有零点，求实数的取值范围.

Answer 1

【答案】(Ⅰ) ；(Ⅱ)答案见解析；(Ⅲ) （Ⅳ）.

【解析】试题分析：（1）根据奇函数性质得，解得值；（2）根据单调性定义，作差通分，根据指数函数单调性确定因子符号，最后根据差的符号确定单调性（3）根据奇偶性以及单调性将不等式化为一元二次不等式恒成立问题，利用判别式求实数的取值范围；（4）根据奇偶性以及单调性将方程转化为一元二次方程有解问题，根据二次函数图像与性质求值域，即得实数的取值范围.

试题解析：（Ⅰ）由题设，需，∴，∴，

经验证， 为奇函数，∴.

（Ⅱ）减函数

证明：任取， ，且，则，

∵

∴

∴， ；

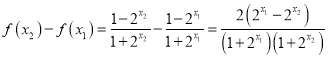
∴，即

∴该函数在定义域上是减函数.

（Ⅲ）由得，

∵是奇函数，∴，

由（Ⅱ）知， 是减函数

∴原问题转化为，即对任意恒成立，

∴，得即为所求.

（Ⅳ）原函数零点的问题等价于方程

由（Ⅱ）知， ，即方程有解

∵，

∴当时函数存在零点.

点睛:利用函数性质解不等式：首先根据函数的性质把不等式转化为的形式，然后根据函数的单调性去掉“”，转化为具体的不等式(组)，此时要注意与的取值应在外层函数的定义域内.