题目内容
【题目】某校从参加高二年级期末考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下频率分布表.根据相关信息回答下列问题: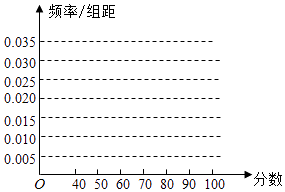
(1)求a,b的值,并画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数在[60,80)内学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人的分数在[70,80)内的概率.
【答案】
(1)解:a=6,b=0.25
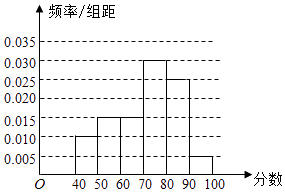
(2)解:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
(3)解:由题意知[60,70)中抽2人,[70,80)中抽取4人,则任取两人共有 ![]() =15种取法(10分)
=15种取法(10分)
至多有一人在[70,80)总有9种情况 ![]() …(12分)
…(12分)
答:分数在[70,80)内的频率为0.3,本次考试的平均分为71,至多有1人的分数在[70,80)内的概率为 ![]()
【解析】(1)求得a,b的值,再画出频率分布直方图;(2)常用组区间的中点值代表该组数据,再估计本次考试的平均分数;(3)先求出基本事件的个数,再利用古典概型的概率求得所给事件的概率.
【考点精析】本题主要考查了分层抽样的相关知识点,需要掌握先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本才能正确解答此题.

练习册系列答案
相关题目