题目内容
某中学将 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班 人,吴老师采用
人,吴老师采用 、
、 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下:
记成绩不低于 分者为“成绩优秀”.
分者为“成绩优秀”.
(1)在乙班样本的 个个体中,从不低于
个个体中,从不低于 分的成绩中随机抽取
分的成绩中随机抽取 个,记随机变量
个,记随机变量 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;
(2)由以上统计数据填写下面 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
| | 甲班( 方式) 方式) | 乙班( 方式) 方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
(1)详见解析;(2)详见解析
解析试题分析:(1)先确定乙班样本 (12分)(2011•福建)某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下: 通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表: 已知某地每单位面积菜地年平均使用氮肥量x(kg)与每单位面积蔬菜年平均产量y(t)之间的关系有如下数据: 已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002, ,800进行编号; 个个体中不低于
个个体中不低于 分成绩中“成绩优秀”的人数,并确定随机变量
分成绩中“成绩优秀”的人数,并确定随机变量 的可能取值,最后根据超几何分布的特点求出随机变量在相应取值下的概率,并列举出随机变量
的可能取值,最后根据超几何分布的特点求出随机变量在相应取值下的概率,并列举出随机变量 的概率分布列,求出其数学期望即可;(2)先根据题中的信息填写
的概率分布列,求出其数学期望即可;(2)先根据题中的信息填写 列联表,并根据表中数据计算
列联表,并根据表中数据计算 的值,查临界值求出犯错误的概率,从而确定有多少把握认为“成绩优秀”与教学方式有关.
的值,查临界值求出犯错误的概率,从而确定有多少把握认为“成绩优秀”与教学方式有关.
试题解析:(1)由题意得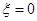 、
、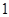 、
、 ,
,
故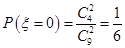 ,
,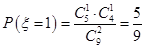 ,
,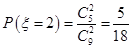 ,
,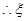 的分布列为:
的分布列为:
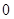
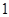


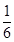
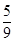
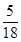
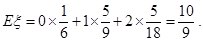
(2)由已知数据得 甲班(  方式)
方式)乙班(  方式)
方式)总计 成绩优秀 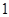
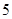
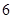
成绩不优秀 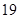

考点同步解读系列答案
同步导学创新学习系列答案
学习总动员单元复习专项复习期末复习系列答案
课时周测月考系列答案
课时练课时笔记系列答案
课时练加考评系列答案
汇文图书卓越课堂系列答案
全程突破系列答案
同步拓展与训练系列答案
升级创优卷系列答案
(Ⅰ)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;X 1 2 3 4 5 f a 0.2 0.45 b c
(Ⅱ)在(Ⅰ)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
附:
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
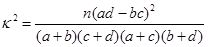
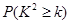
0.050
0.010
0.001

3.841
6.635
10.828
试考查大学生“爱好该项运动是否与性别有关”,若有关,请说明有多少把握。
(1)求x与y之间的相关系数,并检验是否线性相关;年份 1985 1986 1987 1988 1989 1990 1991 1992 x(kg) 70 74 80 78 85 92 90 95 y(t) 5.1 6.0 6.8 7.8 9.0 10.2 10.0 12.0 年份 1993 1994 1995 1996 1997 1998 1999 x(kg) 92 108 115 123 130 138 145 y(t) 11.5 11.0 11.8 12.2 12.5 12.8 13.0
(2)若线性相关,求蔬菜产量y与使用氮肥量x之间的回归直线方程,并估计每单位面积施肥150 kg时,每单位面积蔬菜的年平均产量.
(已知数据: =101,
=101, ≈10.113 3,
≈10.113 3, =161 125,
=161 125, =1 628.55,
=1 628.55, =16 076.8)
=16 076.8)
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)
(2)抽取的100的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42,若在该样本中,数学成绩优秀率是30%,求a,b的值:
(3)在地理成绩及格的学生中,已知人数
数学
优秀
良好
及格
地理
优秀
7
20
5
良好
9
18
6
及格
a
4
b
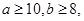 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.
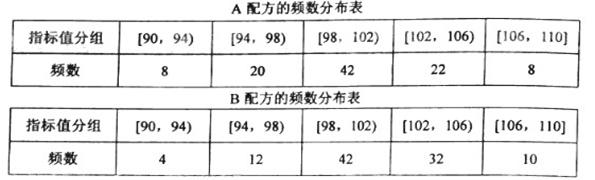
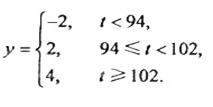
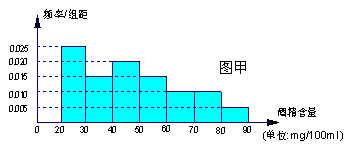
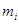 与
与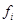 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率) 
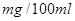 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90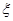 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求
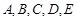 五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为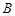 的考生有
的考生有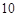 人.
人. 
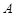 的人数;
的人数; 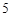 分,
分,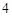 分,
分,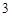 分,
分,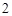 分,
分, 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;