��Ŀ����
��12�֣���2011•������ij����Ʒ����ҵ�������ֳ�����ȼ����ȼ�ϵ��X����Ϊ1��2��3��4��5���ִ�һ��������Ʒ�������ȡ20��������ȼ�ϵ������ͳ�Ʒ������õ�Ƶ�ʷֲ������£�
| X | 1 | 2 | 3 | 4 | 5 |
| f | a | 0.2 | 0.45 | b | c |
�����ڣ��������£����ȼ�ϵ��Ϊ4��3������Ʒ��Ϊx1��x2��x3���ȼ�ϵ��Ϊ5��2������Ʒ��Ϊy1��y2���ִ�x1��x2��x3��y1��y2����5������Ʒ����ȡ�������ٶ�ÿ������Ʒ��ȡ���Ŀ�������ͬ����д�����п��ܵĽ������������������Ʒ�ĵȼ�ϵ��ǡ����ȵĸ��ʣ�
����a=0.1��b=0.15��c=0.1����P��A��=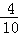 =0.4
=0.4
���������������I��ͨ��Ƶ�ʷֲ������Ƴ�a+b+c=0.35�����õȼ�ϵ��Ϊ4��ǡ��3�����ȼ�ϵ��Ϊ5��ǡ��2�����ֱ����b��c��Ȼ�����a��
��II�����������г������������еĻ����¼�����������x1��x2��x3��y1��y2����5������Ʒ����ȡ�������ȼ�ϵ����ȡ����¼�������⼴�ɣ�
�⣺��I����Ƶ�ʷֲ�����a+0.2+0.45+b+c=1����a+b+c=0.35��
��Ϊ��ȡ��20������Ʒ�У��ȼ�ϵ��Ϊ4��ǡ��3��������b=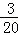 =0.15
=0.15
�ȼ�ϵ��Ϊ5��ǡ��2��������c=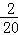 =0.1
=0.1
�Ӷ�a=0.35��0.1��0.15=0.1
����a=0.1��b=0.15��c=0.1��
��II����x1��x2��x3��y1��y2����5������Ʒ����ȡ���������п��ܵĽ��Ϊ��
{x1��x2}��{x1��x3}��{x1��y1}��{x1��y2}��{x2��x3}��{x2��y1}��{x2��y2}��{x3��y1}��{x3��y2}��{y1��y2}
���¼�A��ʾ����x1��x2��x3��y1��y2����5������Ʒ����ȡ�������ȼ�ϵ����ȡ�����A�����Ļ����¼�Ϊ��
{x1��x2}��{x1��x3}��{x2��x3}��{y1��y2}��4����
�ֻ����¼�������Ϊ��10
������ĸ���P��A��=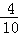 =0.4
=0.4
���������⿼����ʡ�ͳ�ƵȻ���֪ʶ���������ݴ�������������������Ӧ����ʶ�����麯���뷽��˼�롢����������˼�롢��Ȼ���Ȼ˼�룮

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�����С������12�֣�һ���������ס��ҡ���������ʽ�ı���,ÿ����ʽ���� ��
�� �����ͺţ�ij��IJ������ұ�����λ������������ʽ�ֲ�����ķ���������������ı����г�ȡ
�����ͺţ�ij��IJ������ұ�����λ������������ʽ�ֲ�����ķ���������������ı����г�ȡ ���������м���ʽ����
���������м���ʽ���� ��.
��.
| �ͺ� | ����ʽ | ����ʽ | ����ʽ |
 |  |  |  |
 |  |  |  |
��1����
 ��ֵ��
��ֵ�� ��2���÷ֲ�����ķ����ڼ���ʽ�����г�ȡһ������Ϊ
 ���������������������ȡ
���������������������ȡ �����ӣ���������
�����ӣ��������� ��
�� ���ӵĸ��ʣ�
���ӵĸ��ʣ� ij�����ζ�ȫ��50��ѧ��ѧϰ�����ԺͶԴ��༶������̬�Ƚ����˵���,ͳ���������±���ʾ��
| | �����μӰ༶���� | ��̫�����μӰ༶���� | �ϼ� |
| ѧϰ�����Ը� | 18 | 7 | 25 |
| ѧϰ������һ�� | 6 | 19 | 25 |
| �ϼ� | 24 | 26 | 50 |
(1)���������������һ��ѧ��,��ô�鵽�����μӰ༶������ѧ���ĸ����Ƕ��٣��鵽��̫�����μӰ༶������ѧϰ������һ���ѧ���ĸ����Ƕ��٣�
(2)�����ö����Լ����˼�뷽���㲦��ѧ����ѧϰ��������Դ��༶������̬���Ƿ��й�ϵ����˵�����ɣ�(�ο��±�)
| P(K2��k) | 0��50 | 0��40 | 0��25 | 0��15 | 0��10 | 0��05 | 0��025 | 0��010 | 0��005 | 0��001 |
| k | 0��455 | 0��708 | 1��323 | 2��072 | 2��706 | 3��841 | 5��024 | 6��635 | 7��879 | 10��828 |
ij�ֲ�Ʒ�Ĺ�����֧��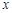 ����Ԫ�������۶�
����Ԫ�������۶�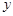 ����Ԫ��֮�������µĶ�Ӧ���ݣ�
����Ԫ��֮�������µĶ�Ӧ���ݣ�
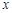 | 2 | 4 | 5 | 6 | 8 |
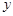 | 30 | 40 | 60 | 50 | 70 |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
��1������ɢ��ͼ��
��2����ع�ֱ�߷��̣�
��3���ݴ˹��ƹ�����Ϊ9��Ԫʱ����������
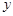 ��ֵ��
��ֵ���ο���ʽ���ع�ֱ�ߵķ���
 ������
������ ��
�� Ϊ���˽��һ�꼶ѧ�������������ijУ��10%�ı�����ȫУ800����һ�꼶ѧ�����Ա���г�����飬�õ�����Ƶ���ֲ�����
��1����������Ƶ���ֲ���
| ���ߣ�cm�� | [160,165�� | [165,170�� | [170,175�� | [175,180�� | [180,185�� | [185,190] |
| Ƶ�� | 2 | 5 | 14 | 13 | 4 | 2 |
��2����������Ƶ���ֲ���
| ���ߣ�cm�� | [150,155�� | [150,160�� | [160,165�� | [165,170�� | [170,175�� | [175,180] |
| Ƶ�� | 2 | 12 | 16 | 6 | 3 | 1 |
��1���ֱ���Ƹ�һ�꼶������Ů����ƽ�����ߣ�
��2���������У�������180cm���ϵ���������ѡ2�ˣ���������һ��������185cm���ϵĸ���.
ij��ѧ�� ����һ�����ֳ�ˮƽ��ͬ�ļס���������ƽ�аࡱ��ÿ��
����һ�����ֳ�ˮƽ��ͬ�ļס���������ƽ�аࡱ��ÿ�� �ˣ�����ʦ����
�ˣ�����ʦ���� ��
�� ���ֲ�ͬ�Ľ�ѧ��ʽ�ֱ��ڼס�����������н�ѧʵ��.Ϊ�˽��ѧЧ������ĩ���Ժֱ�������༶�и������ȡ
���ֲ�ͬ�Ľ�ѧ��ʽ�ֱ��ڼס�����������н�ѧʵ��.Ϊ�˽��ѧЧ������ĩ���Ժֱ�������༶�и������ȡ ��ѧ���ijɼ�����ͳ�ƣ������ľ�Ҷͼ���£�
��ѧ���ijɼ�����ͳ�ƣ������ľ�Ҷͼ���£�
�dzɼ������� ����Ϊ���ɼ����㡱.
����Ϊ���ɼ����㡱.
��1�����Ұ������� �������У��Ӳ�����
�������У��Ӳ����� �ֵijɼ��������ȡ
�ֵijɼ��������ȡ �������������
������������� Ϊ�鵽���ɼ����㡱�ĸ�������
Ϊ�鵽���ɼ����㡱�ĸ������� �ķֲ��м���ѧ����
�ķֲ��м���ѧ���� ��
��
��2��������ͳ��������д���� �����������ж��ж�������Ϊ���ɼ����㡱���ѧ��ʽ�йأ�
�����������ж��ж�������Ϊ���ɼ����㡱���ѧ��ʽ�йأ�
| | �װࣨ ��ʽ�� ��ʽ�� | �Ұࣨ ��ʽ�� ��ʽ�� | �ܼ� |
| �ɼ����� | | | |
| �ɼ������� | | | |
| �ܼ� | | | |

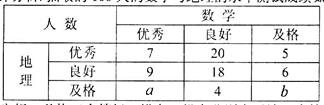
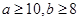 �����ڵ����ɼ������ѧ���У���ѧ�ɼ�����������ȼ���������ٵĸ���.
�����ڵ����ɼ������ѧ���У���ѧ�ɼ�����������ȼ���������ٵĸ���.