题目内容
15.已知等差数列{an}和单调递减数列{bn}(n∈N*),{bn}通项公式为bn=λn2+a7•n.若a3,a11是方程x2-x-2=0的两根,则实数λ的取值范围是( )| A. | (-∞,-3) | B. | (−∞,−16) | C. | (−16,+∞) | D. | (-3,+∞) |
分析 根据等差数列的性质,结合根与系数之间的关系进行求解即可.
解答 解::∵a3,a11是x2-x-2=0的两根,
∴a3+a11=1.(或两根为2,-1⇒a3+a11=1)
∵{an}是等差数列,
∴a3+a11=2a7⇒a7=12,
∴bn=λn2+12n.
∵{bn}递减,∴bn+1-bn<0对n∈N*恒成立,⇒λ(n+1)2+12(n+1)−(λn2+12n)<0⇒λ(2n+1)+12<0,
∴λ<−14n+2对n∈N*恒成立.
∵(−14n+2)min=−16,∴λ<−16.
故选:B.
点评 本题主要考查数列的函数性质,结合等差数列,以及根与系数之间的关系是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
10.函数f(x)=-3x在区间[1,2]上的最小值是( )
| A. | -9 | B. | -6 | C. | -3 | D. | -13 |
20.在直角坐标系中,A(-2,3),B(3,-2),沿x轴把直角坐标系折成120°的二面角,则AB的长度为( )
| A. | √2 | B. | 4√2 | C. | 3√2 | D. | 2√11 |
7.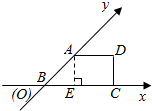 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )| A. | 2+2√2 | B. | 4+2√2 | C. | 1+√2 | D. | 1+√2 |
4.抛掷两颗均匀的正方体骰子,所得的两个点数中一个恰是另一个的两倍的概率是( )
| A. | 14 | B. | 16 | C. | 18 | D. | 112 |
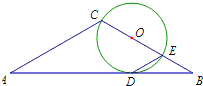 如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.
如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.