题目内容
如图,在平面直角坐标系 中,过
中,过 轴正方向上一点
轴正方向上一点 任作一直线,与抛物线
任作一直线,与抛物线 相交于
相交于 两点.一条垂直于
两点.一条垂直于 轴的直线,分别与线段
轴的直线,分别与线段 和直线
和直线 交于点
交于点 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 为线段
为线段 的中点,求证:
的中点,求证: 为此抛物线的切线;
为此抛物线的切线;
(3)试问(2)的逆命题是否成立?说明理由.
 中,过
中,过 轴正方向上一点
轴正方向上一点 任作一直线,与抛物线
任作一直线,与抛物线 相交于
相交于 两点.一条垂直于
两点.一条垂直于 轴的直线,分别与线段
轴的直线,分别与线段 和直线
和直线 交于点
交于点 .
.(1)若
 ,求
,求 的值;
的值;(2)若
 为线段
为线段 的中点,求证:
的中点,求证: 为此抛物线的切线;
为此抛物线的切线;(3)试问(2)的逆命题是否成立?说明理由.

解:(1)设直线 的方程为
的方程为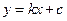 ,
,
将该方程代入 得
得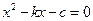 .
.
令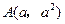 ,
,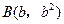 ,则
,则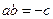 .
.
因为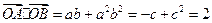 ,解得
,解得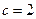 ,
,
或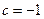 (舍去).故
(舍去).故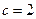 .
.
(2)由题意知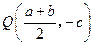 ,直线
,直线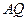 的斜率为
的斜率为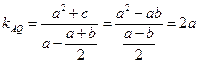 .
.
又 的导数为
的导数为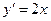 ,所以点
,所以点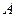 处切线的斜率为
处切线的斜率为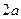 ,
,
因此,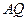 为该抛物线的切线.
为该抛物线的切线.
(3)(2)的逆命题成立,证明如下:
设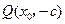 .
.
若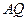 为该抛物线的切线,则
为该抛物线的切线,则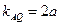 ,
,
又直线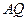 的斜率为
的斜率为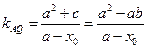 ,所以
,所以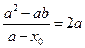 ,
,
得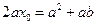 ,因
,因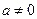 ,有
,有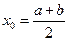 .
.
故点 的横坐标为
的横坐标为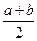 ,即
,即 点是线段
点是线段 的中点.
的中点.
 的方程为
的方程为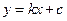 ,
,将该方程代入
 得
得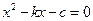 .
.令
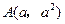 ,
,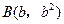 ,则
,则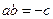 .
.因为
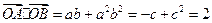 ,解得
,解得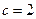 ,
,或
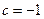 (舍去).故
(舍去).故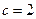 .
.(2)由题意知
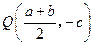 ,直线
,直线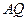 的斜率为
的斜率为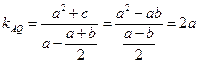 .
.又
 的导数为
的导数为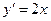 ,所以点
,所以点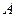 处切线的斜率为
处切线的斜率为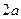 ,
,因此,
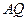 为该抛物线的切线.
为该抛物线的切线.(3)(2)的逆命题成立,证明如下:
设
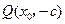 .
.若
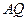 为该抛物线的切线,则
为该抛物线的切线,则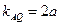 ,
,又直线
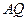 的斜率为
的斜率为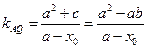 ,所以
,所以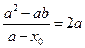 ,
,得
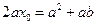 ,因
,因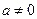 ,有
,有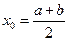 .
.故点
 的横坐标为
的横坐标为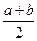 ,即
,即 点是线段
点是线段 的中点.
的中点. 略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
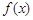 =Atan(
=Atan( x+
x+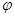 )(
)(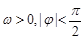 ),y=
),y=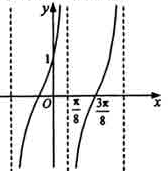
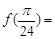


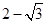
 ,f’(x)>2,则f(x)>2x+4的解集为( )
,f’(x)>2,则f(x)>2x+4的解集为( ) )
)
 ,若
,若 ,则
,则 .
.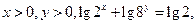 则
则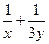 的最小值是 .
的最小值是 .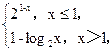 则满足f(x)≤2的x的取值范围是( )
则满足f(x)≤2的x的取值范围是( ) )
) 的大致图象,则
的大致图象,则 等于( )
等于( ) B
B  C
C  D
D 

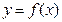 和
和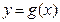 在
在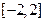 的图象如下所示:
的图象如下所示: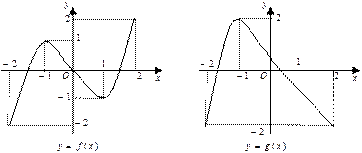
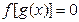 有且仅有 个根.
有且仅有 个根.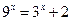 的解为 ▲ .
的解为 ▲ .