题目内容
已知函数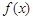 =Atan(
=Atan(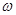 x+
x+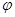 )(
)(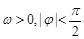 ),y=
),y=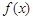 的部分图像如下图,
的部分图像如下图,
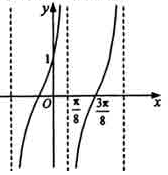
则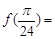
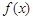 =Atan(
=Atan(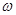 x+
x+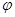 )(
)(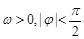 ),y=
),y=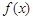 的部分图像如下图,
的部分图像如下图,
则
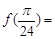
A.2+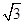 | B.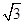 |
C.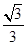 | D.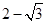 |
B
根据函数的图象,求出函数的周期,然后求出ω,确定A的值,根据( ,0)求出φ的值,图象经过(0.1)确定A的值,求出函数的解析式,然后求出f(
,0)求出φ的值,图象经过(0.1)确定A的值,求出函数的解析式,然后求出f( )即可.
)即可.
解:由题意可知T= ,所以ω=2,
,所以ω=2,
函数的解析式为:f(x)=Atan(ωx+φ),因为函数过( ,0)所以0=Atan(
,0)所以0=Atan( +φ)所以φ=
+φ)所以φ= ,
,
图象经过(0,1),所以,1=Atan ,所以A=1,所以f(x)=tan(2x+
,所以A=1,所以f(x)=tan(2x+ )则f(
)则f( )=tan(
)=tan( +
+ )=
)=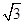
故答案为:B
 ,0)求出φ的值,图象经过(0.1)确定A的值,求出函数的解析式,然后求出f(
,0)求出φ的值,图象经过(0.1)确定A的值,求出函数的解析式,然后求出f( )即可.
)即可.解:由题意可知T=
 ,所以ω=2,
,所以ω=2,函数的解析式为:f(x)=Atan(ωx+φ),因为函数过(
 ,0)所以0=Atan(
,0)所以0=Atan( +φ)所以φ=
+φ)所以φ= ,
,图象经过(0,1),所以,1=Atan
 ,所以A=1,所以f(x)=tan(2x+
,所以A=1,所以f(x)=tan(2x+ )则f(
)则f( )=tan(
)=tan( +
+ )=
)=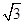
故答案为:B

练习册系列答案
相关题目
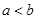 ,函数
,函数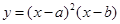 的图像可能是( )
的图像可能是( )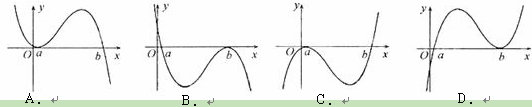
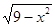 -k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )
-k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )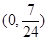
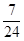 ,+∞)
,+∞)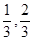 )
)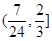
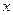 与玩具B的个数
与玩具B的个数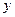 表示每天的利润
表示每天的利润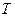 元;
元; ,
, ,
, ,
, .记
.记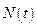 为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数
为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数



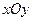 中,过
中,过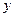 轴正方向上一点
轴正方向上一点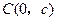 任作一直线,与抛物线
任作一直线,与抛物线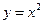 相交于
相交于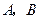 两点.一条垂直于
两点.一条垂直于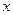 轴的直线,分别与线段
轴的直线,分别与线段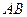 和直线
和直线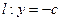 交于点
交于点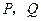 .
.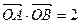 ,求
,求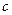 的值;
的值;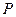 为线段
为线段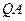 为此抛物线的切线;
为此抛物线的切线;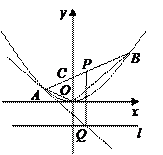
 其中
其中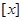 表示不超过
表示不超过 的最大整数,如
的最大整数,如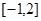 =-2,
=-2,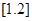 =1,
=1, =1,若直线y=
=1,若直线y= 与函数y=
与函数y= 的图象恰有三个不同的交点,则
的图象恰有三个不同的交点,则 的取值范围是
的取值范围是
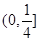


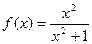 ,
,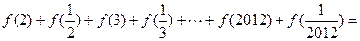 .
. 若有
若有 则
则 的取值范围为( )
的取值范围为( )


