题目内容
【题目】某玩具所需成本费用为P元，且P＝1 000＋5x＋
x2，而每套售出的价格为Q元，其中Q(x)＝a＋
(a，b∈R)，
(1)问：玩具厂生产多少套时，使得每套所需成本费用最少？
(2)若生产出的玩具能全部售出，且当产量为150套时利润最大，此时每套价格为30元，求a，b的值．(利润＝销售收入－成本)．
【答案】（1）该玩具厂生产100套时每套所需成本最少．（2）a＝25，b＝30.
【解析】
（1）先建立每套所需成本费用函数关系式，再根据基本不等式求最值，（2）先根据利润＝销售收入－成本建立利润函数关系式，再根据二次函数性质确定开口方向、对称轴位置以及最大值取法，解方程与不等式组可得a，b的值.
解：(1)每套玩具所需成本费用为
＝
＝
x＋
＋5≥2
＋5＝25，
当x＝，即x＝100时等号成立，
故该玩具厂生产100套时每套所需成本最少．
(2)设售出利润为w，则w＝x·Q(x)－P
＝x
－
＝
x2＋(a－5)x－1 000，
由题意得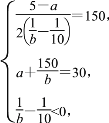
解得a＝25，b＝30.
练习册系列答案
名校课堂系列答案
相关题目
