题目内容
已知函数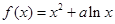
(Ⅰ)当a=﹣2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)=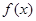 +
+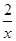 在
在 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.
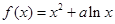
(Ⅰ)当a=﹣2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)=
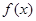 +
+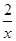 在
在 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.(Ⅰ)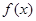 的单调递增区间是(1,+∞),
的单调递增区间是(1,+∞),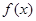 的单调递减区间是(0, 1).
的单调递减区间是(0, 1).
(Ⅱ)实数a的取值范围 0,+∞)
0,+∞)
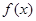 的单调递增区间是(1,+∞),
的单调递增区间是(1,+∞),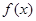 的单调递减区间是(0, 1).
的单调递减区间是(0, 1).(Ⅱ)实数a的取值范围
 0,+∞)
0,+∞)本试题主要是考查了导数在研究函数中的 运用。以及函数单调性的逆向的运用
(1)根据函数的定义域,然后结合导数,导数的符号与函数单调性的关系求解得到单调区间。
(2)利用g(x)=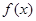 +
+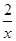 在
在 1,+∞)上是单调函数,则
1,+∞)上是单调函数,则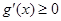 在
在 1,+∞)上恒成立,然后分离参数的思想求解其范围。解:(Ⅰ)
1,+∞)上恒成立,然后分离参数的思想求解其范围。解:(Ⅰ)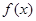 的单调递增区间是(1,+∞),
的单调递增区间是(1,+∞),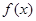 的单调递减区间是(0, 1).
的单调递减区间是(0, 1).
(Ⅱ)由题意得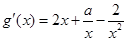 ,函数g(x)在
,函数g(x)在 1,+∞)上是单调函数.
1,+∞)上是单调函数.
① 若函数g(x)为 1,+∞)上的单调增函数,则
1,+∞)上的单调增函数,则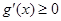 在
在 1,+∞)上恒成立,
1,+∞)上恒成立,
即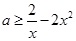 在
在 1, +∞)上恒成立,设
1, +∞)上恒成立,设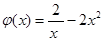 ,∵
,∵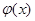 在
在 1,+∞)上单调递减,
1,+∞)上单调递减,
∴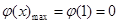 ,∴a≥0
,∴a≥0
②若函数g(x)为 1,+∞)上的单调减函数,则
1,+∞)上的单调减函数,则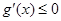 在
在 1,+∞)上恒成立,不可能.
1,+∞)上恒成立,不可能.
∴实数a的取值范围 0,+∞)
0,+∞)
(1)根据函数的定义域,然后结合导数,导数的符号与函数单调性的关系求解得到单调区间。
(2)利用g(x)=
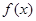 +
+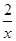 在
在 1,+∞)上是单调函数,则
1,+∞)上是单调函数,则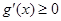 在
在 1,+∞)上恒成立,然后分离参数的思想求解其范围。解:(Ⅰ)
1,+∞)上恒成立,然后分离参数的思想求解其范围。解:(Ⅰ)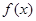 的单调递增区间是(1,+∞),
的单调递增区间是(1,+∞),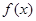 的单调递减区间是(0, 1).
的单调递减区间是(0, 1).(Ⅱ)由题意得
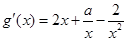 ,函数g(x)在
,函数g(x)在 1,+∞)上是单调函数.
1,+∞)上是单调函数.① 若函数g(x)为
 1,+∞)上的单调增函数,则
1,+∞)上的单调增函数,则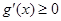 在
在 1,+∞)上恒成立,
1,+∞)上恒成立,即
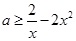 在
在 1, +∞)上恒成立,设
1, +∞)上恒成立,设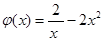 ,∵
,∵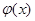 在
在 1,+∞)上单调递减,
1,+∞)上单调递减,∴
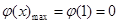 ,∴a≥0
,∴a≥0②若函数g(x)为
 1,+∞)上的单调减函数,则
1,+∞)上的单调减函数,则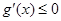 在
在 1,+∞)上恒成立,不可能.
1,+∞)上恒成立,不可能.∴实数a的取值范围
 0,+∞)
0,+∞)
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 .
. 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件;
上递增的充分而不必要的条件; 时,满足
时,满足 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中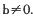
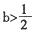 时,判断函数
时,判断函数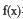 在定义域上的单调性;
在定义域上的单调性;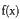 的极值点;
的极值点;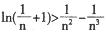 都成立.
都成立.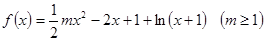 .
.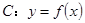 在点
在点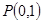 处的切线
处的切线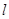 与曲线
与曲线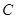 有且只有一个公共点,求
有且只有一个公共点,求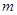 的值;
的值;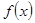 存在单调递减区间
存在单调递减区间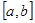 ,并求出单调递减区间的长度
,并求出单调递减区间的长度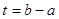 的取值范围.
的取值范围.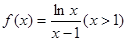
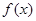 的单调性;
的单调性; 、使得关于
、使得关于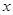 的不等式
的不等式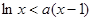 在(1,
在(1,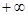 )上恒成立,若存在,求出
)上恒成立,若存在,求出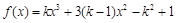 在区间(0,3)是增函数,则k的取值范围是( )
在区间(0,3)是增函数,则k的取值范围是( )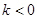
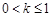
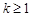

 (a≠0)
(a≠0) ,e]的最大值;
,e]的最大值;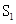 为直线
为直线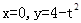 (
(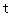 为常数)及
为常数)及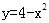 所围成的图形的面积,
所围成的图形的面积,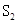 为直线
为直线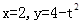 (
(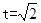 时,求
时,求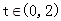 ,求
,求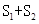 的最小值。
的最小值。
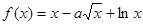 (
(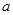 为常数)在定义域上是增函数,则实数
为常数)在定义域上是增函数,则实数