题目内容
设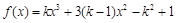 在区间(0,3)是增函数,则k的取值范围是( )
在区间(0,3)是增函数,则k的取值范围是( )
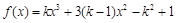 在区间(0,3)是增函数,则k的取值范围是( )
在区间(0,3)是增函数,则k的取值范围是( )A.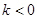 | B.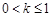 |
C.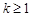 | D. |
C
解:f'(x)=3kx2+6(k-1)x,
∵函数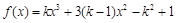 在区间(0,3)上是增函数,
在区间(0,3)上是增函数,
∴f'(x)=3kx2+6(k-1)x》0在区间(0,3)上恒成立
当k=0时,成立
k>0时,f'(4)=12k+6(k-1)×4》0,即k》1
k<0时,f'(4)=12k+6(k-1)×40,f'(0)》0,k>0
故k的取值范围是k》1
∵函数
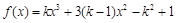 在区间(0,3)上是增函数,
在区间(0,3)上是增函数,∴f'(x)=3kx2+6(k-1)x》0在区间(0,3)上恒成立
当k=0时,成立
k>0时,f'(4)=12k+6(k-1)×4》0,即k》1
k<0时,f'(4)=12k+6(k-1)×40,f'(0)》0,k>0
故k的取值范围是k》1

练习册系列答案
相关题目
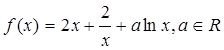 。
。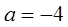 ,求函数
,求函数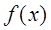 的单调区间;
的单调区间;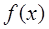 在
在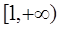 上单调递增,求实数
上单调递增,求实数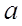 的取值范围;
的取值范围;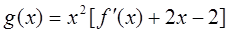 ,若
,若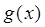 的最小值是
的最小值是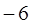 ,求函数
,求函数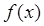 的解析式。
的解析式。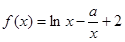 。
。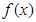 的单调区间;
的单调区间;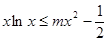 在
在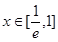 上恒成立,求
上恒成立,求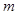 的取值范围。
的取值范围。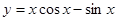 在下列哪个区间内是增函数( )
在下列哪个区间内是增函数( )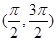
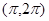
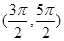
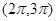
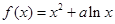
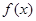 +
+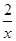 在
在 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.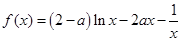 .
.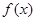 的单调性;
的单调性;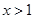 时,
时,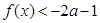 ,求实数
,求实数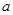 的取值范围;
的取值范围;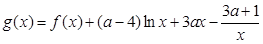 ,若
,若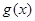 在区间
在区间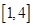 上不单调, 求实数
上不单调, 求实数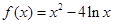 ,
,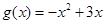 ;
;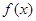 在
在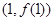 处的切线方程;
处的切线方程;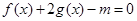 有唯一解,求
有唯一解,求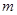 的取值范围;
的取值范围;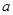 ,使得
,使得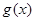 在
在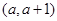 上均为增函数,若存在求出
上均为增函数,若存在求出