题目内容
抛物线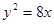 上一点P到
上一点P到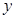 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )
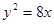 上一点P到
上一点P到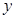 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )| A.4 | B.6 | C.8 | D.12 |
B
试题分析:由方程可知准线为
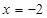 ,P到
,P到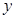 轴的距离是4,所以P到准线的距离为6,由抛物线定义可知P到该抛物线焦点的距离是6
轴的距离是4,所以P到准线的距离为6,由抛物线定义可知P到该抛物线焦点的距离是6点评:抛物线上的点到焦点的距离与其到准线的距离相等,利用这一点可实现两距离的转化

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
题目内容
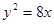 上一点P到
上一点P到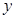 轴的距离是4,则点P到该抛物线焦点的距离是( )
轴的距离是4,则点P到该抛物线焦点的距离是( )| A.4 | B.6 | C.8 | D.12 |
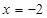 ,P到
,P到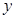 轴的距离是4,所以P到准线的距离为6,由抛物线定义可知P到该抛物线焦点的距离是6
轴的距离是4,所以P到准线的距离为6,由抛物线定义可知P到该抛物线焦点的距离是6
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案