Question

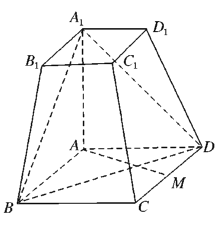
【题目】函数的图象与直线y＝a恰有三个不同的交点，求实数a的取值范围.

Answer 1

【答案】.

【解析】

由题意得f′(x)＝x2－4＝(x＋2)(x－2)，得出函数f(x)的单调区间和极值，作出函数f(x)的大致图象，根据函数图象可得出答案.

∵f(x)＝x3－4x＋4，∴f′(x)＝x2－4＝(x＋2)(x－2)．

令f′(x)＝0，得x＝2或x＝－2.当x变化时，f′(x)，f(x)的变化情况如下表：

x	(－∞，－2)	－2	(－2，2)	2	(2，＋∞)
f′(x)	＋	0	－	0	＋
f(x)	↗	极大值	↘	极小值	↗

∴当x＝－2时，函数取得极大值f(－2)＝；

当x＝2时，函数取得极小值f(2)＝－

且f(x)在(－∞，－2)上单调递增，在(－2，2)上单调递减，在(2，＋∞)上单调递增．

根据函数单调性、极值情况，它的图象大致如图所示，

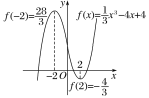
结合图象知