题目内容
【题目】设函数![]() .
.
(1)求函数![]() 的极值点个数;
的极值点个数;
(2)若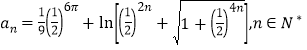 ,证明
,证明![]()
![]() .
.
【答案】(1)2个(2)详见解析
【解析】
(1)由![]() 是奇函数,把问题转化成
是奇函数,把问题转化成![]() 的极值点个数问题,求出
的极值点个数问题,求出![]() ,把
,把![]() 的正负问题转化成
的正负问题转化成![]() 正负来处理,求出
正负来处理,求出![]() ,判断
,判断![]() 的单调性,结合函数零点判断方法即可判断在区间
的单调性,结合函数零点判断方法即可判断在区间![]() 上存在唯一的
上存在唯一的![]() 使
使![]() .在
.在![]() 上不存在
上不存在![]() 使得
使得![]() ,问题得解。
,问题得解。
(2)利用(1)中的结论可知:![]() 在区间
在区间![]() 内恒成立.令
内恒成立.令![]() ,可将问题转化成
,可将问题转化成![]()
![]() ,问题得证。
,问题得证。
解:(1)因为![]() 为奇函数,其图像关于原点对称,所以只需考虑
为奇函数,其图像关于原点对称,所以只需考虑![]() 上的极值点个数,
上的极值点个数,
![]() ,
,![]() 时,
时,
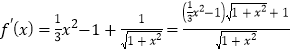 .
.
令![]() ,
,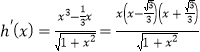 ,
,
∴当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
∴![]() .
.
取![]() ,
,![]() ,
,
∴在区间![]() 上存在唯一的
上存在唯一的![]() 使
使![]() .
.
∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
又![]() 为奇函数,
为奇函数,
∴![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
∴![]() 的极值点共2个.
的极值点共2个.
(2)由(1)可知![]() 在区间
在区间![]() 内单调递减,且
内单调递减,且![]() 恒成立.
恒成立.
∴![]() 时,
时,![]() ,
,
即得![]() .
.
又令![]() ,
,
得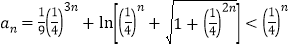 .
.
∴![]()
![]()
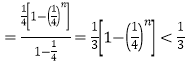

【题目】王府井百货分店今年春节期间,消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对春节前7天参加抽奖活动的人数进行统计,![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该活动只持续10天,估计共有多少名顾客参加抽奖.
参与公式: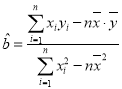 ,
,![]() ,
,![]() .
.
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
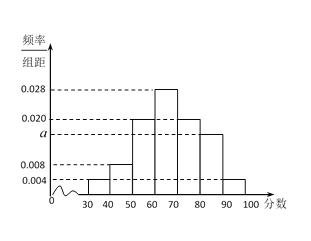
【题目】改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
(Ⅰ)求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
(Ⅱ)已知交通安全意识强的样本中男女比例为4:1,完成2×2列联表,并判断有多大把握认为交通安全意识与性别有关;
(Ⅲ)在(Ⅱ)的条件下,从交通安全意识强的驾驶员中随机抽取2人,求抽到的女性人数![]() 的分布列及期望.
的分布列及期望.
附: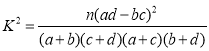 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
①先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用
的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,
元的人数,![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,随机变量
元的人数,随机变量![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
②小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
