题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{sinx,}&{x≤1}\\{f(x-1),}&{x>1}\end{array}\right.$,则f($\frac{4}{3}$)的值为$sin\frac{1}{3}$.分析 利用f($\frac{4}{3}$)=$f(\frac{4}{3}-1)$=$f(\frac{1}{3})$即可得出.
解答 解:f($\frac{4}{3}$)=$f(\frac{4}{3}-1)$=$f(\frac{1}{3})$=sin$\frac{1}{3}$.
故答案为:sin$\frac{1}{3}$.
点评 本题查克拉分段函数的求值,考查了计算能力,属于基础题.

练习册系列答案
相关题目
16.己知cos31°=a,则sin239°•tan149°的值是( )
| A. | $\frac{1-{a}^{2}}{a}$ | B. | $\sqrt{1-{a}^{2}}$ | C. | $\frac{{a}^{2}-1}{a}$ | D. | -$\sqrt{1-{a}^{2}}$ |
18.已知集合M={x|0≤x≤2},N={x|x-2=0},则下列说法正确的是( )
| A. | N∈M | B. | N⊆M | C. | M⊆N | D. | M∈N |
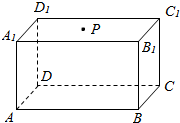 如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l
如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l