题目内容
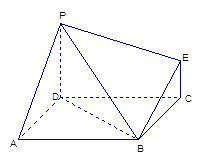
(本小题满分12分)如图,在四面体 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.

(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)若平面 ⊥平面
⊥平面 ,且
,且 ,求三棱锥
,求三棱锥 的体积.
的体积.
 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
(1)求证:平面
 ⊥平面
⊥平面 ;
;(2)若平面
 ⊥平面
⊥平面 ,且
,且 ,求三棱锥
,求三棱锥 的体积.
的体积.(1)见解析;(2)  。
。
 。
。本试题主要是考查了面面垂直的证明以及三棱锥的体积的求解的综合运用
(1)因为 分别是
分别是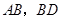 的中点,
的中点,
∴ ∥
∥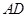 .
.
又 ,∴
,∴  .
.
∵ ,∴
,∴ .
.
∵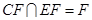 ,∴
,∴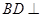 面
面 ,进而由面面垂直的判定定理得到结论。
,进而由面面垂直的判定定理得到结论。
(2)∵ 面
 面
面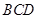 ,且
,且 ,
,
∴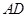
 面
面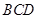 .
.
由 和
和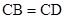 ,得
,得 是正三角形.
是正三角形.
得到底面积和高,进而求解体积。
解:(1)∵ 分别是
分别是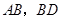 的中点,
的中点,
∴ ∥
∥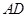 .
.
又 ,∴
,∴  .
.
∵ ,∴
,∴ .
.
∵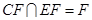 ,∴
,∴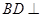 面
面 .
.
∵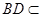 面
面 ,∴平面
,∴平面 平面
平面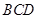 .…6分
.…6分
(2) ∵ 面
 面
面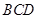 ,且
,且 ,
,
∴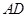
 面
面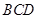 .
.
由 和
和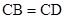 ,得
,得 是正三角形.
是正三角形.
所以 .
.
所以 . ………12分
. ………12分
(1)因为
 分别是
分别是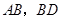 的中点,
的中点,∴
 ∥
∥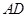 .
.又
 ,∴
,∴  .
.∵
 ,∴
,∴ .
.∵
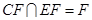 ,∴
,∴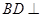 面
面 ,进而由面面垂直的判定定理得到结论。
,进而由面面垂直的判定定理得到结论。(2)∵ 面

 面
面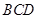 ,且
,且 ,
, ∴
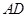
 面
面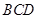 .
.由
 和
和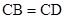 ,得
,得 是正三角形.
是正三角形. 得到底面积和高,进而求解体积。
解:(1)∵
 分别是
分别是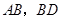 的中点,
的中点,∴
 ∥
∥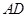 .
.又
 ,∴
,∴  .
.∵
 ,∴
,∴ .
.∵
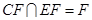 ,∴
,∴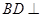 面
面 .
.∵
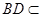 面
面 ,∴平面
,∴平面 平面
平面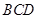 .…6分
.…6分(2) ∵ 面

 面
面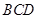 ,且
,且 ,
, ∴
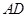
 面
面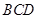 .
.由
 和
和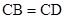 ,得
,得 是正三角形.
是正三角形. 所以
 .
. 所以
 . ………12分
. ………12分
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
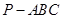 中,
中,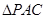 和
和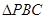 是边长为
是边长为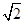 的等边三角形,
的等边三角形,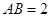 ,
,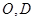 分别是
分别是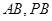 的中点.
的中点.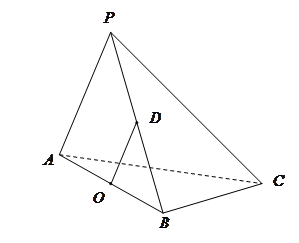
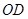 ∥平面
∥平面 ;
;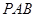 ⊥平面
⊥平面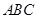 ;
; 平面
平面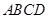 ,
,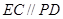 ,且
,且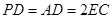 ="2" .
="2" . 平面
平面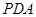 ;
;
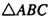 是正三角形,AD
是正三角形,AD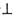 平面ABC,AD=2AB=6,则该球的体积为 ( )
平面ABC,AD=2AB=6,则该球的体积为 ( )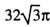 B.
B.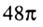 C.
C.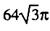 D.
D.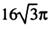
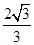 π
π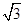 π
π  π
π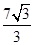 π
π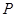 在圆柱
在圆柱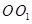 的底面圆
的底面圆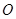 上,
上,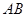 为圆
为圆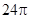 ,
, ,
,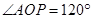 。
。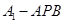 的体积。
的体积。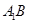 与
与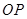 所成角的余弦值;
所成角的余弦值;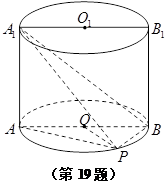
 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱 底面
底面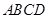 ,且
,且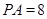 ,则该四棱锥的体积是( )
,则该四棱锥的体积是( )