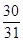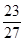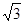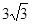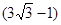题目内容
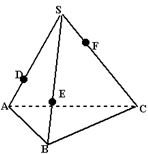
(本小题满分12分)如图所示多面体中,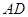 ⊥平面
⊥平面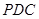 ,
,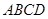 为平行四边形,
为平行四边形,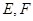 分别为
分别为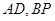 的中点,
的中点,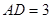 ,
,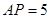 ,
,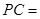
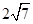 .
.
(1)求证: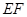 ∥平面
∥平面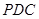 ;
;
(2)若∠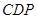 =90°,求证
=90°,求证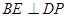 ;
;
(3)若∠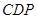 =120°,求该多面体的体积.
=120°,求该多面体的体积.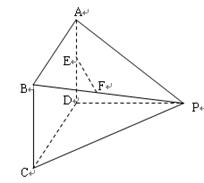
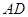 ⊥平面
⊥平面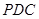 ,
,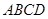 为平行四边形,
为平行四边形,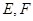 分别为
分别为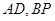 的中点,
的中点,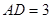 ,
,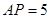 ,
,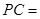
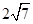 .
.(1)求证:
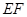 ∥平面
∥平面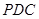 ;
;(2)若∠
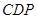 =90°,求证
=90°,求证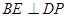 ;
;(3)若∠
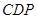 =120°,求该多面体的体积.
=120°,求该多面体的体积.
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)该五面体的体积为 。
。
 。
。(Ⅰ)取PC的中点为O,连FO,DO,可证FO∥ED,且FO=ED,所以四边形EFOD是平行四边形,从而可得EF∥DO,利用线面平行的判定,可得EF∥平面PDC;
(Ⅱ)先证明PD⊥平面ABCD,再证明BE⊥DP;
(Ⅲ)连接AC,由ABCD为平行四边形可知△ABC与△ADC面积相等,所以三棱锥P-ADC与三棱锥P-ABC体积相等,即五面体的体积为三棱锥P-ADC体积的二倍.
(Ⅰ)取PC的中点为O,连FO,DO,∵F,O分别为BP,PC的中点,
∴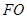 ∥BC,且
∥BC,且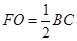 ,又ABCD为平行四边形,
,又ABCD为平行四边形,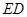 ∥BC,且
∥BC,且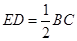 ,
,
∴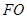 ∥ED,且
∥ED,且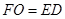
∴四边形EFOD是平行四边形 --------------------------------2分
即EF∥DO 又EF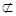 平面PDC ∴EF∥平面PDC. ---------------------- 4分
平面PDC ∴EF∥平面PDC. ---------------------- 4分
(Ⅱ)若∠CDP=90°,则PD⊥DC,又AD⊥平面PDC ∴AD⊥DP,
∴PD⊥平面ABCD, ------------- 6分
∵BE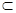 平面ABCD,∴BE⊥DP ------------ 8分
平面ABCD,∴BE⊥DP ------------ 8分
(Ⅲ)连结AC,由ABCD为平行四边形可知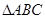 与
与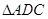 面积相等,
面积相等,
所以三棱锥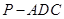 与三棱锥
与三棱锥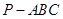 体积相等,
体积相等,
即五面体的体积为三棱锥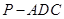 体积的二倍.
体积的二倍.
∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4又∠CDP=120°PC=2 ,
,
由余弦定理并整理得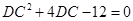 , 解得DC=2 ------------------- 10分
, 解得DC=2 ------------------- 10分
∴ 三棱锥
三棱锥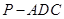 的体积
的体积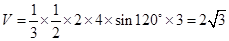
∴该五面体的体积为 -------------------- 12分
-------------------- 12分
(Ⅱ)先证明PD⊥平面ABCD,再证明BE⊥DP;
(Ⅲ)连接AC,由ABCD为平行四边形可知△ABC与△ADC面积相等,所以三棱锥P-ADC与三棱锥P-ABC体积相等,即五面体的体积为三棱锥P-ADC体积的二倍.
(Ⅰ)取PC的中点为O,连FO,DO,∵F,O分别为BP,PC的中点,
∴
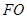 ∥BC,且
∥BC,且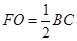 ,又ABCD为平行四边形,
,又ABCD为平行四边形,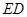 ∥BC,且
∥BC,且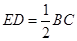 ,
,∴
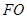 ∥ED,且
∥ED,且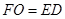
∴四边形EFOD是平行四边形 --------------------------------2分
即EF∥DO 又EF
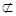 平面PDC ∴EF∥平面PDC. ---------------------- 4分
平面PDC ∴EF∥平面PDC. ---------------------- 4分(Ⅱ)若∠CDP=90°,则PD⊥DC,又AD⊥平面PDC ∴AD⊥DP,
∴PD⊥平面ABCD, ------------- 6分
∵BE
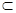 平面ABCD,∴BE⊥DP ------------ 8分
平面ABCD,∴BE⊥DP ------------ 8分(Ⅲ)连结AC,由ABCD为平行四边形可知
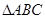 与
与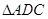 面积相等,
面积相等,所以三棱锥
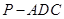 与三棱锥
与三棱锥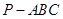 体积相等,
体积相等,即五面体的体积为三棱锥
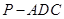 体积的二倍.
体积的二倍.∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4又∠CDP=120°PC=2
 ,
,由余弦定理并整理得
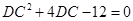 , 解得DC=2 ------------------- 10分
, 解得DC=2 ------------------- 10分∴
 三棱锥
三棱锥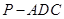 的体积
的体积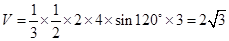
∴该五面体的体积为
 -------------------- 12分
-------------------- 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
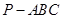 中,
中,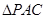 和
和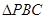 是边长为
是边长为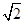 的等边三角形,
的等边三角形,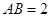 ,
,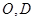 分别是
分别是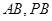 的中点.
的中点.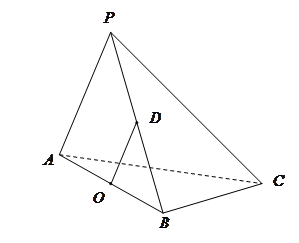
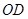 ∥平面
∥平面 ;
;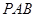 ⊥平面
⊥平面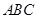 ;
;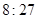 ,那么这两个球的表面积的比为 .
,那么这两个球的表面积的比为 . ,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )
,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )