题目内容
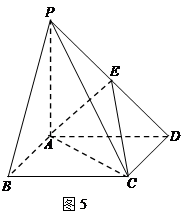
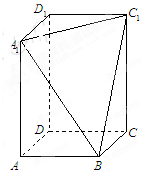
如图5,在四棱锥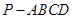 中,底面
中,底面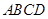 为正方形,
为正方形,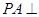 平面
平面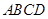 ,
,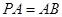 ,点
,点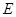 是
是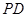 的中点.
的中点.
(1)求证: //平面
//平面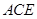 ;
;
(2)若四面体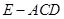 的体积为
的体积为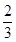 ,求
,求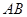 的长.
的长.
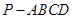 中,底面
中,底面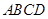 为正方形,
为正方形,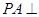 平面
平面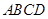 ,
,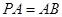 ,点
,点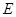 是
是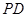 的中点.
的中点.
(1)求证:
 //平面
//平面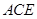 ;
;(2)若四面体
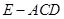 的体积为
的体积为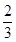 ,求
,求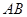 的长.
的长.(1)见解析(2)2
本试题主要是考查了立体几何中线面平行的判定和椎体体积的求解的综合运用。
(1)由于四棱锥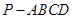 中,底面
中,底面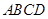 为正方形,
为正方形,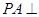 平面
平面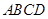 ,
,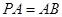 ,点
,点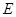 是
是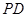 的中点.利用条件得到
的中点.利用条件得到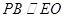 ,从而得证。
,从而得证。
(2)将锥体的底面积和高求解得到,进而得到体积的值。
(1)证明:连接 交
交 于点
于点 ,连接
,连接 ,
,
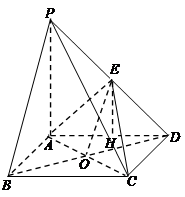
因为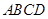 是正方形,所以点
是正方形,所以点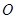 是
是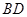 的中点.
的中点.
因为点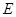 是
是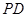 的中点,
的中点,
所以 是△
是△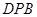 的中位线.
的中位线.
所以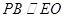 .
.
因为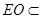 平面
平面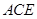 ,
,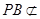 平面
平面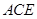 ,
,
所以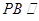 平面
平面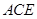 .
.
(2)解:取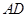 的中点
的中点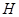 ,连接
,连接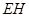 , 因为点
, 因为点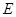 是
是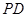 的中点,所以
的中点,所以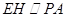 .
.
因为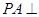 平面
平面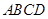 ,所以
,所以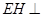 平面
平面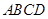 .
.
设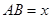 ,则
,则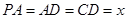 ,且
,且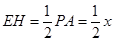 .
.
所以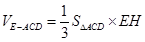
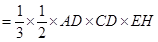
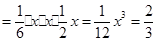 .
.
解得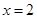 . 故
. 故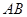 的长为2.
的长为2.
(1)由于四棱锥
 中,底面
中,底面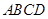 为正方形,
为正方形,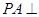 平面
平面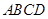 ,
,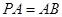 ,点
,点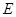 是
是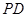 的中点.利用条件得到
的中点.利用条件得到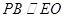 ,从而得证。
,从而得证。(2)将锥体的底面积和高求解得到,进而得到体积的值。
(1)证明:连接
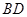 交
交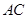 于点
于点 ,连接
,连接 ,
,
因为
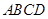 是正方形,所以点
是正方形,所以点 是
是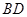 的中点.
的中点.因为点
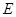 是
是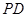 的中点,
的中点,所以
 是△
是△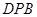 的中位线.
的中位线.所以
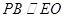 .
. 因为
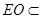 平面
平面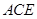 ,
,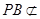 平面
平面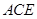 ,
,所以
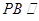 平面
平面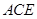 .
.(2)解:取
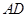 的中点
的中点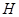 ,连接
,连接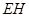 , 因为点
, 因为点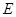 是
是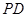 的中点,所以
的中点,所以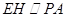 .
. 因为
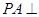 平面
平面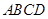 ,所以
,所以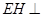 平面
平面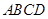 .
. 设
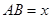 ,则
,则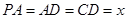 ,且
,且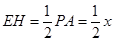 .
. 所以
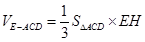
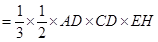
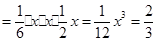 .
. 解得
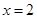 . 故
. 故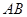 的长为2.
的长为2. 
练习册系列答案
相关题目
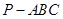 中,
中,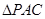 和
和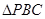 是边长为
是边长为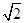 的等边三角形,
的等边三角形,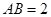 ,
,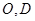 分别是
分别是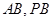 的中点.
的中点.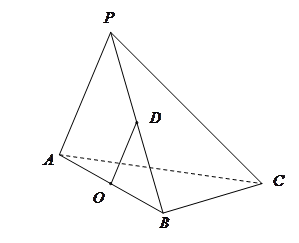
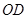 ∥平面
∥平面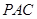 ;
;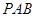 ⊥平面
⊥平面 ;
;


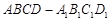 中,
中,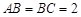 ,过
,过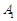 、
、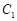 、
、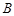 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体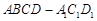 ,且这个几何体的体积为
,且这个几何体的体积为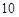 .
.
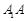 的长;
的长;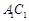 的中点为
的中点为 ,求异面直线
,求异面直线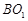 与
与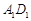 所成角的余弦值.
所成角的余弦值.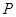 在圆柱
在圆柱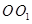 的底面圆
的底面圆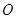 上,
上,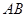 为圆
为圆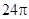 ,
,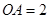 ,
,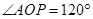 。
。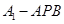 的体积。
的体积。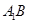 与
与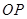 所成角的余弦值;
所成角的余弦值;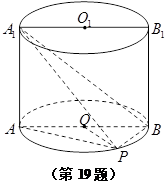
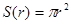 ,周长
,周长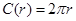 ,若将
,若将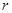 看作是
看作是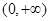 上的变量,则
上的变量,则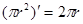 ……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为
……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为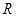 的球,若将
的球,若将 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个鸡蛋蛋巢,将表面积为4
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个鸡蛋蛋巢,将表面积为4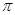 的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与鸡蛋巢底面的距离为___________.
的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与鸡蛋巢底面的距离为___________.