题目内容
2.若函数f(x)=|mx2-(2m+1)x+m+3|恰有4个单调区间,则实数m的取值范围为( )| A. | (-∞,$\frac{1}{8}$) | B. | (-∞,0)∪(0,$\frac{1}{8}$) | C. | (0,$\frac{1}{8}$] | D. | ($\frac{1}{8}$,1] |
分析 根据二次函数的单调性的性质进行求解即可.
解答 解:若f(x)=|mx2-(2m+1)x+m+3|恰有4个单调区间,
则等价为函数y=mx2-(2m+1)x+m+3与x轴有两个不同的交点,
即m≠0且判别式△=(2m+1)2-4m(m+3)>0,
即4m2+4m+1-4m2-12m>0,
即-8m+1>0,
解得m<$\frac{1}{8}$且m≠0,
即实数m的取值范围为(-∞,0)∪(0,$\frac{1}{8}$),
故选:B.
点评 本题主要考查函数单调性的应用,根据一元二次函数的性质转化为判别式△的关系是解决本题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
17.若函数y=x2-3x-4的定义域为[a,b],值域为[-$\frac{25}{4}$,-4].则下列说法正确的是( )
| A. | a=0,b=0 | B. | 若a∈(0,$\frac{3}{2}$),则b∈($\frac{3}{2}$,3) | ||
| C. | 若a=0,则b∈(3,+∞) | D. | 若a∈(0,$\frac{3}{2}$),则b=3 |
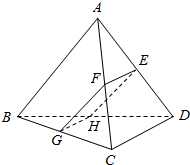 如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.
如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.