题目内容
14.已知tan($\frac{π}{4}$+α)=$\frac{1}{7}$,α∈($\frac{π}{2}$,π),则tanα的值是-$\frac{3}{4}$;sin2α+sinαcosα的值是$-\frac{3}{25}$; $cos({α-\frac{π}{6}})$的值是$\frac{{3-4\sqrt{3}}}{10}$.分析 由已知及两角和的正切函数公式可得tan($\frac{π}{4}$+α)=$\frac{1+tanα}{1-tanα}$=$\frac{1}{7}$,即可解得tanα的值,利用同角三角函数关系式可得sin2α+sinαcosα=$\frac{si{n}^{2}α+sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+tanα}{ta{n}^{2}α+1}$即可求值;由范围α∈($\frac{π}{2}$,π),
可求cosα=-$\sqrt{\frac{1}{1+ta{n}^{2}α}}$,sinα的值,利用两角差的余弦函数公式即可求值.
解答 解:∵tan($\frac{π}{4}$+α)=$\frac{1+tanα}{1-tanα}$=$\frac{1}{7}$,∴解得:tanα=-$\frac{3}{4}$,
∴sin2α+sinαcosα=$\frac{si{n}^{2}α+sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+tanα}{ta{n}^{2}α+1}$=$-\frac{3}{25}$.
∵α∈($\frac{π}{2}$,π),
∴cosα=-$\sqrt{\frac{1}{1+ta{n}^{2}α}}$=-$\frac{4}{5}$,sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{3}{5}$
∴$cos({α-\frac{π}{6}})$=$\frac{\sqrt{3}}{2}$cos$α+\frac{1}{2}sinα$=$\frac{\sqrt{3}}{2}×(-\frac{4}{5})$+$\frac{1}{2}×\frac{3}{5}$=$\frac{{3-4\sqrt{3}}}{10}$.
故答案为:-$\frac{3}{4}$,$-\frac{3}{25}$,$\frac{{3-4\sqrt{3}}}{10}$.
点评 本题主要考查了两角和的正切函数公式,同角三角函数关系式,两角差的余弦函数公式在三角函数求值中的应用,考查了计算能力,属于基础题.

| A. | 4 | B. | 2$\sqrt{3}$ | C. | 1 | D. | 4$\sqrt{3}$ |
| A. | (-∞,$\frac{1}{8}$) | B. | (-∞,0)∪(0,$\frac{1}{8}$) | C. | (0,$\frac{1}{8}$] | D. | ($\frac{1}{8}$,1] |
| A. | 2550 | B. | 2600 | C. | 2651 | D. | 2652 |
| A. | ?x∈R,x2<x+1 | B. | ?x∈R,x2≥x+1 | ||
| C. | ?x∈R,?y∈R,xy2=y2 | D. | ?x∈R,?y∈R,x>y2 |
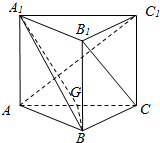 如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.
如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.