题目内容
17.已知f(x)=$\left\{{\begin{array}{l}{{x^2}+1,x≥0}\\{-2x,x<0}\end{array}}$,(1)求f(0)和f[f(0)]的值;
(2)若f(x0)=10,求出x0所有可能取的值.
分析 (1)利用分段函数直接求解函数值即可.
(2)利用分段函数列出方程求解即可.
解答 解:(1)f(x)=$\left\{{\begin{array}{l}{{x^2}+1,x≥0}\\{-2x,x<0}\end{array}}$,
∴f(0)=1,f(f(0))=2(4分)
$(2)\left\{{\begin{array}{l}{{x_0}≥0}\\{{x_0}^2+1=10}\end{array}}\right.$或$\left\{{\begin{array}{l}{{x_0}<0}\\{-2{x_0}=10}\end{array}}\right.$.∴x0=3或x0=-5(8分)
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
2.若函数f(x)=|mx2-(2m+1)x+m+3|恰有4个单调区间,则实数m的取值范围为( )
| A. | (-∞,$\frac{1}{8}$) | B. | (-∞,0)∪(0,$\frac{1}{8}$) | C. | (0,$\frac{1}{8}$] | D. | ($\frac{1}{8}$,1] |
9.已知数列{an}中,a1=a2=1,且an+2-an=1,则数列{an}的前100项和为( )
| A. | 2550 | B. | 2600 | C. | 2651 | D. | 2652 |
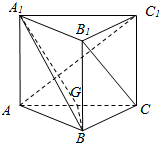 如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.
如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.