题目内容
10.函数y=($\frac{1}{4}$)x+($\frac{1}{2}$)x-1(x≤-1)的值域是[8,+∞).分析 配方便可得到$y=[(\frac{1}{2})^{x}+1]^{2}-1$,从而根据x≤-1可以得出$(\frac{1}{2})^{x}$的范围,从而得到$[(\frac{1}{2})^{x}+1]^{2}$的范围,进一步得到y的范围,即得出该函数的值域.
解答 解:$y=(\frac{1}{2})^{2x}+2•(\frac{1}{2})^{x}=[(\frac{1}{2})^{x}+1]^{2}-1$;
x≤-1;
∴$(\frac{1}{2})^{x}≥(\frac{1}{2})^{-1}=2$;
∴$[(\frac{1}{2})^{x}+1]^{2}≥9$;
∴y≥8;
∴该函数的值域为[8,+∞).
故答案为:[8,+∞).
点评 考查函数值域的概念,配方处理二次式子的方法,以及指数函数的单调性,根据不等式的性质求值域.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
2.若函数f(x)=|mx2-(2m+1)x+m+3|恰有4个单调区间,则实数m的取值范围为( )
| A. | (-∞,$\frac{1}{8}$) | B. | (-∞,0)∪(0,$\frac{1}{8}$) | C. | (0,$\frac{1}{8}$] | D. | ($\frac{1}{8}$,1] |
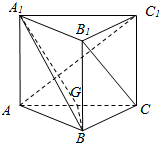 如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.
如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.