题目内容
4.函数y=$\frac{\sqrt{1-{x}^{2}}}{2+x}$的值域是[0,$\frac{\sqrt{3}}{3}$].分析 函数y=$\frac{\sqrt{1-{x}^{2}}}{2+x}$的几何意义是点(-2,0)与点(x,$\sqrt{1-{x}^{2}}$)连线的斜率,利用数形结合求解.
解答 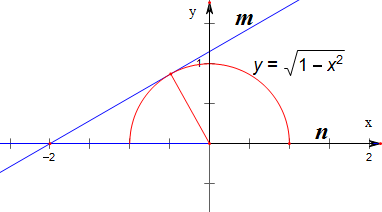 解:函数y=$\frac{\sqrt{1-{x}^{2}}}{2+x}$的几何意义是点(-2,0)与点(x,$\sqrt{1-{x}^{2}}$)连线的斜率,
解:函数y=$\frac{\sqrt{1-{x}^{2}}}{2+x}$的几何意义是点(-2,0)与点(x,$\sqrt{1-{x}^{2}}$)连线的斜率,
作图如右图,
直线n的斜率为0,直线m的斜率为$\frac{\sqrt{3}}{3}$;
故函数y=$\frac{\sqrt{1-{x}^{2}}}{2+x}$的值域是[0,$\frac{\sqrt{3}}{3}$],
故答案为:[0,$\frac{\sqrt{3}}{3}$].
点评 本题考查了函数的值域的求法及数形结合的思想应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的个数有( )
| A. | 600 | B. | 464 | C. | 300 | D. | 210 |
19.函数y=(a2-3a+3)ax是指数函数,则a的值为( )
| A. | 1或2 | B. | 1 | ||
| C. | 2 | D. | a>0且a≠1的所有实数 |