题目内容
【题目】若函数 ![]() 的定义域为A,函数g(x)=lg(x﹣1),x∈[2,11]的值域为B,则A∩B为( )
的定义域为A,函数g(x)=lg(x﹣1),x∈[2,11]的值域为B,则A∩B为( )
A.(﹣∞,1)
B.(﹣∞,1]
C.[0,1]
D.(0,1]
【答案】C
【解析】解答:∵函数 ![]() ,∴1﹣x≥0,
,∴1﹣x≥0,
∴x≤1,
∴A={x|x≤1},
∵g(x)=lg(x﹣1),x∈[2,11]
∵g(x)在x∈[2,11]上为增函数,
∴g(x)∈[0,1],
∴B={x|0≤x≤1},
∴A∩B为[0,1].
故选C.
分析:根据根式有意义的条件,求出函数的定义域A,再根据对数的定义域,求出其值域B,然后两集合取交集.
【考点精析】掌握函数的定义域及其求法和函数的值域是解答本题的根本,需要知道求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知某产品的历史收益率的频率分布直方图如图所示:
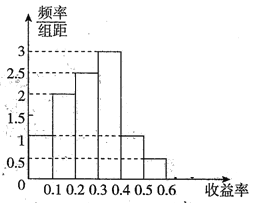
(1)试计算该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
据此计算出的回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从上述五组销量中随机抽取两组,求两组销量中恰有一组超过6万件的概率.
【题目】对甲、乙的学习成绩进行抽样分析,各抽五门功课,得到的观测值如表:
甲 | 60 | 80 | 70 | 90 | 70 |
乙 | 80 | 60 | 70 | 80 | 75 |
问:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?( )
A.甲的平均成绩较好,乙的各门功课发展较平衡
B.甲的平均成绩较好,甲的各门功课发展较平衡
C.乙的平均成绩较好,甲的各门功课发展较平衡
D.乙的平均成绩较好,乙的各门功课发展较平衡