题目内容
已知椭圆的两焦点为F1(0,-1)、F2(0,1),直线y=4是椭圆的一条准线.
(1)求椭圆方程;
(2)设点P在椭圆上,且|PF1|-|PF2|=1,求tan∠F1PF2的值.
(1)求椭圆方程;
(2)设点P在椭圆上,且|PF1|-|PF2|=1,求tan∠F1PF2的值.
(1) 椭圆方程为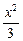 +
+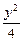 =1.
=1.
(2)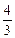
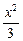 +
+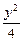 =1.
=1.(2)
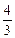
本题考查椭圆的基本性质及解题的综合能力.
(1)设椭圆方程为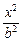 +
+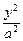 =1(a>b>0).
=1(a>b>0).
由题设知c=1,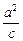 =4,∴a2=4,b2=a2-c2=3.
=4,∴a2=4,b2=a2-c2=3.
∴所求椭圆方程为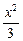 +
+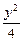 =1.
=1.
(2)由(1)知a2=4,a=2.
由椭圆定义知|PF1|+|PF2|=4,又|PF1|-|PF2|=1,
∴|PF1|=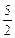 ,|PF2|=
,|PF2|=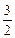 .
.
又|F1F2|=2c=2,
由余弦定理cos∠F1PF2=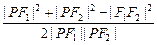 =
=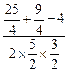 =
=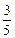 .
.
∴tan∠F1PF2=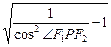 =
=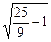 =
=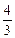 .
.
(1)设椭圆方程为
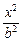 +
+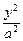 =1(a>b>0).
=1(a>b>0).由题设知c=1,
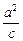 =4,∴a2=4,b2=a2-c2=3.
=4,∴a2=4,b2=a2-c2=3.∴所求椭圆方程为
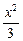 +
+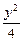 =1.
=1.(2)由(1)知a2=4,a=2.
由椭圆定义知|PF1|+|PF2|=4,又|PF1|-|PF2|=1,
∴|PF1|=
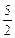 ,|PF2|=
,|PF2|=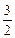 .
.又|F1F2|=2c=2,
由余弦定理cos∠F1PF2=
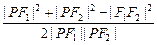 =
=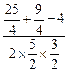 =
=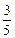 .
.∴tan∠F1PF2=
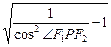 =
=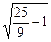 =
=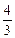 .
.
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点 ,向量
,向量 与
与 是共线向量。
是共线向量。 分别是左、右焦点,求∠
分别是左、右焦点,求∠ 的取值范围;
的取值范围; ,一个焦点是F(-m,0)(m是大于0的常数).
,一个焦点是F(-m,0)(m是大于0的常数). |=2|
|=2| |,求直线l的斜率.
|,求直线l的斜率.




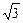 ),椭圆
),椭圆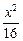 +
+ 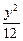 =1的右焦点为F,点P在椭圆上移动.当|PA|+2|PF|取最小值时,P点的坐标是多少?
=1的右焦点为F,点P在椭圆上移动.当|PA|+2|PF|取最小值时,P点的坐标是多少? -
- )
)
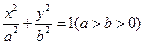 的左焦点
的左焦点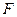 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦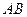 ,若点
,若点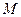 在
在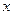 轴上,且使得
轴上,且使得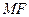 为
为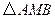 的一条内角平分线,则称点
的一条内角平分线,则称点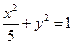 的“左特征点”
的“左特征点” 的离心率为
的离心率为 ,则
,则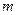 =
=  的内部,则m的取值范围是 ( )
的内部,则m的取值范围是 ( ) <m<
<m<