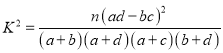题目内容
【题目】已知函数![]() ,(
,( ![]() ,
, ![]() ).
).
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(2)若![]() 时,不等式
时,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,记函数
时,记函数![]() 的导函数
的导函数![]() 的两个零点是
的两个零点是![]() 和
和![]() (
(![]() ),求证:
),求证: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】试题分析:
(1)利用导函数大于零可得函数的单调增区间为![]() ,
, ![]() .
.
(2)不等式恒成立转化为![]() 在区间
在区间![]() 上恒成立,构造新函数
上恒成立,构造新函数![]() ,结合题意讨论其性质可得
,结合题意讨论其性质可得![]() ;
;
(3)由题意可得![]() (
(![]() ),由根与系数的关系:
),由根与系数的关系: ![]() .由题意有
.由题意有
![]() ,
, ![]() ,构造新函数
,构造新函数![]() .利用函数的性质可得
.利用函数的性质可得![]() .
.
试题解析:(1)由题意: ![]() ,
, ![]() ,
, ![]() 时,
时, ![]()
所以![]()
令![]() ,得
,得![]() ,因为
,因为![]() ,所以
,所以![]() 或
或![]()
所以![]() 的单调增区间为
的单调增区间为![]() ,
, ![]()
(2)![]() 时,
时, ![]() ,
,
不等式![]() 在
在![]() 上恒成立即为:
上恒成立即为: ![]() 在区间
在区间![]() 上恒成立
上恒成立
令![]() ,则
,则![]() ,令
,令![]() 得:
得: ![]() ,
,
因为![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
所以![]() ,所以
,所以![]()
(3)方法一:因为![]() ,所以
,所以![]() ,从而
,从而![]() (
(![]() )
)
由题意知, ![]() ,
, ![]() 是方程
是方程![]() 的两个根,故
的两个根,故![]() .
.
记![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]()
![]() ,所以
,所以![]() ,
, ![]() ,且
,且![]() (
(![]() ,
, ![]() ).
).
![]()
因为![]() ,所以
,所以![]() ,
, ![]() .
.
令![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() .
.
方法二:因为![]() ,所以
,所以![]() ,从而
,从而![]() (
(![]() ).
).
由题意知, ![]() ,
, ![]() 是方程
是方程![]() 的两个根.记
的两个根.记![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,且
,且![]() 在
在![]() 上为减函数.
上为减函数.
所以![]() .
.
因为![]() ,故
,故![]() .
.

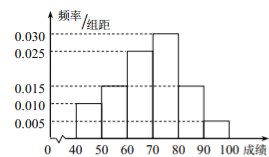
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾, 5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,并作出如下频率分布直方图(图1):
五组,并作出如下频率分布直方图(图1):

(1)试根据频率分布直方图估计小区平均每户居民的平均损失;
(同一组中的数据用该组区间的中点值作代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过6000元的居民中随机
抽出2户进行捐款援助,求抽出的2户居民损失均超过8000元的概率;
(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,
在图2表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额超过或
不超过500元和自身经济损失是否超过4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 | 30 | ||
捐款不超过500元 | 6 | ||
合计 |
附:临界值参考公式:  ,
, ![]() .
.
| 0.15 | 0.10 | 0.05 /td> | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】十八届五种全会公报指出:努力促进人口均衡发展,坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子的政策,提高生殖保健、妇幼保健、托儿等公共服务水平.为了解适龄公务员对放开生育二胎政策的态度,某部门随机调查了100位30到40岁的公务员,得到情况如下表:
男公务员 | 女公务员 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
(1)是否有95%以上的把握认为“生二胎与性别有关”,并说明理由;
(2)把以上频率当概率,若从社会上随机抽取3位30到40岁的男公务员,记其中生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列,数学期望.
的分布列,数学期望.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:![]()
【题目】某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
(Ⅰ)求该企业2016年一年生产一件产品的利润为10的概率;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
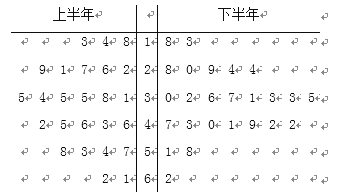
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2=![]() .
.