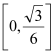题目内容
【题目】我们用圆的性质类比球的性质如下:
①p:圆心与弦(非直径)中点的连线垂直于弦; q:球心与小圆截面圆心的连线垂直于截面.
②p:与圆心距离相等的两条弦长相等; q:与球心距离相等的两个截面圆的面积相等.
③p:圆的周长为C=πd(d是圆的直径); q:球的表面积为S=πd2(d是球的直径).
④p:圆的面积为S=
R·πd(R,d是圆的半径与直径); q:球的体积为V=
R·πd2(R,d是球的半径与直径).
则上面的四组命题中,其中类比得到的q是真命题的有( )个
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】圆与球有以下类似的性质：
（1）圆是平面上一点的距离等于定长的所有点构成的集合，球面是空间中到一定点的距离等于定长的所有点构成的集合.
（2）圆是平面内封闭的曲线所围成的对称图形，球是空间中封闭的曲面所围成的对称图形.
与圆的有关性质相比较，可以推测球的有关性质：
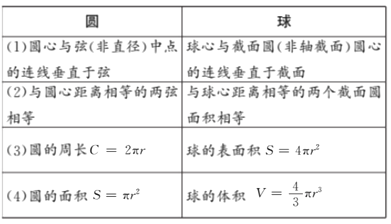
结合题意可知所给的选项都是正确的.
本题选择D选项.
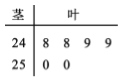
【题目】葫芦岛市某高中进行一项调查：2012年至2016年本校学生人均年求学花销
（单位：万元）的数据如下表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
（1）求
关于
的线性回归方程；
（2）利用（1）中的回归方程，分析2012年至2016年本校学生人均年求学花销的变化情况，并预测该地区2017年本校学生人均年求学花销情况．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
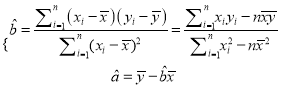
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇，2016年双11期间，某平台的销售业绩高达918亿人民币，与此同时，相关管理部门也推出了针对电商的商品和服务评价体系，现从评价系统中随机选出200次成功的交易，并对其评价结果进行统计，对商品的好评率为
，对服务的好评率为
，其中对商品和服务都做出好评的交易为80次.
在犯错误概率不超过（ ）的前提下，认为商品好评与服务好评有关.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. 
B. 
C. 
D. 