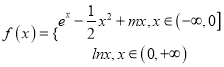题目内容
【题目】已知函数![]() .
.
(1)设![]() ,
,
①记![]() 的导函数为
的导函数为![]() ,求
,求![]() ;
;
②若方程![]() 有两个不同实根,求实数
有两个不同实根,求实数![]() 的取值范围;
的取值范围;
(2)若在![]() 上存在一点
上存在一点![]() 使
使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)①对![]() 进行求导,将
进行求导,将![]() 代入可得
代入可得![]() 的值,
的值,
试题解析: ![]() 的定义域
的定义域![]() ,
, ![]() 的定义域为
的定义域为![]() ,
,
(1)①![]() ,∴
,∴![]() ;②对
;②对![]() 进行二次求导,判断
进行二次求导,判断![]() 的单调性得其符号,从而可得
的单调性得其符号,从而可得![]() 的单调性,结合图象的大致形状可得
的单调性,结合图象的大致形状可得![]() 的取值范围;(2)将题意转化为
的取值范围;(2)将题意转化为![]() ,令
,令![]() ,题意等价于
,题意等价于![]() 在
在![]() 上的最小值小于0,对
上的最小值小于0,对![]() 进行求导,对导函数进行分类讨论,判断单调性得其最值.
进行求导,对导函数进行分类讨论,判断单调性得其最值.
②![]() ,∴
,∴![]() 递增,又
递增,又![]() ,所以
,所以![]() 在
在![]() 上递减,
上递减, ![]() 递增。又
递增。又![]() 趋于0的时候,
趋于0的时候, ![]() 趋于6;
趋于6; ![]() 趋于
趋于![]() 的时候,
的时候, ![]() 趋于
趋于![]() ,又
,又![]() ,所以
,所以![]() ;
;
(2)由题可得![]() ,∴
,∴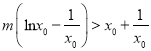 ,∴
,∴![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上的最小值小于0,
上的最小值小于0,
又![]() ,
,
1,当![]() 时,即
时,即![]() ,
, ![]() 在
在![]() 上递减,所以
上递减,所以![]() ,解得
,解得![]() ;
;
2,当![]() 即
即![]() ,
, ![]() 在
在![]() 递增,∴
递增,∴![]() 解得
解得![]() ;
;
3,当![]() ,即
,即![]() ,此时要求
,此时要求![]() 又
又![]() ,
,
所以![]() ,
,
所以![]() 此时
此时![]() 不成立,
不成立,
综上![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇,2016年双11期间,某平台的销售业绩高达918亿人民币,与此同时,相关管理部门也推出了针对电商的商品和服务评价体系,现从评价系统中随机选出200次成功的交易,并对其评价结果进行统计,对商品的好评率为![]() ,对服务的好评率为
,对服务的好评率为![]() ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.
在犯错误概率不超过( )的前提下,认为商品好评与服务好评有关.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某工厂的甲、乙两个车间的![]() 名工人进行了劳动技能大比拼,规定:技能成绩大于或等于
名工人进行了劳动技能大比拼,规定:技能成绩大于或等于![]() 分为优秀,
分为优秀, ![]() 分以下为非优秀,统计成成绩后,得到如下的
分以下为非优秀,统计成成绩后,得到如下的![]() 列联表,且已知在甲、乙两个车间工人中随机抽取
列联表,且已知在甲、乙两个车间工人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲车间 |
| ||
乙车间 |
| ||
合计 |
|
(1)请完成上面的列联表;
(2)根据列联表的数据,若按![]() 的可靠性要求,能否认为“成绩与车间有关系”?
的可靠性要求,能否认为“成绩与车间有关系”?