题目内容
.已知函数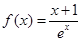 .
.
(1)求函数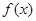 的单调区间;
的单调区间;
(2)设函数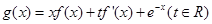 .是否存在实数
.是否存在实数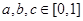 ,使得
,使得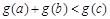 ?若存在,求实数
?若存在,求实数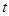 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
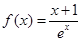 .
. (1)求函数
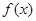 的单调区间;
的单调区间;(2)设函数
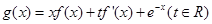 .是否存在实数
.是否存在实数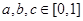 ,使得
,使得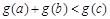 ?若存在,求实数
?若存在,求实数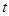 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.(1)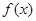 在区间
在区间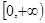 上是减函数,
上是减函数,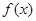 在区间
在区间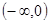 上是增函数;
上是增函数;
(2)Ⅰ.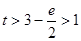 ;
;
Ⅱ. ;
;
Ⅲ.存在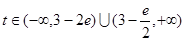 使得命题成立。
使得命题成立。
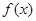 在区间
在区间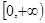 上是减函数,
上是减函数,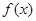 在区间
在区间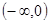 上是增函数;
上是增函数;(2)Ⅰ.
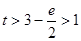 ;
;Ⅱ.
 ;
;Ⅲ.存在
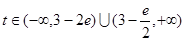 使得命题成立。
使得命题成立。(1)求导,利用导数大(小)于零,求出其单调递增(减)区间.
(2)假设存在,函数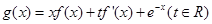 ,实数
,实数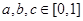 ,使得
,使得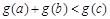 .解决此问题的关键是把此问题转化为
.解决此问题的关键是把此问题转化为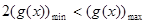 ,
,
然后利用导数研究其最值即可.
(1)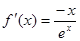 -----------------2分
-----------------2分
当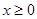 时,
时,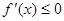 ,
,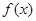 在区间
在区间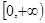 上是减函数
上是减函数
当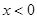 时,
时,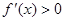 ,
,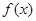 在区间
在区间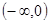 上是增函数---------------4分
上是增函数---------------4分
(2)假设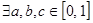 ,使得
,使得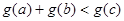 ,则
,则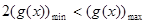 -----------5分
-----------5分
由条件知: ,
,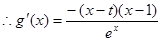 ------------------6分
------------------6分
Ⅰ.当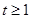 时,
时,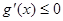 ,
,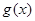 在
在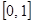 上单调递减,
上单调递减,
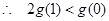 ,即
,即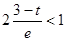 ,得:
,得: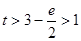 -----------7分
-----------7分
Ⅱ.当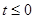 时,
时,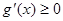 ,
,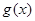 在
在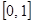 上单调递增
上单调递增
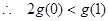 ,即
,即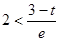 ,得:
,得: -----------8分
-----------8分
Ⅲ.当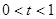 时
时
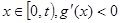 ,
,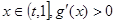 ,所以:
,所以: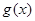 在
在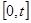 单调递减,在
单调递减,在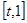 上单调递增
上单调递增
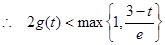 ,即
,即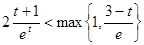 --------------------10分
--------------------10分
由(1)知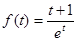 在
在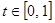 上单调递减,故有
上单调递减,故有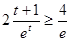
而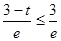 ,所以无解.
,所以无解.
综上所述:存在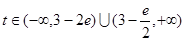 使得命题成立--------12分
使得命题成立--------12分
(2)假设存在,函数
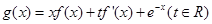 ,实数
,实数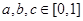 ,使得
,使得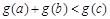 .解决此问题的关键是把此问题转化为
.解决此问题的关键是把此问题转化为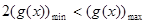 ,
,然后利用导数研究其最值即可.
(1)
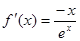 -----------------2分
-----------------2分当
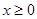 时,
时,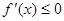 ,
,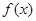 在区间
在区间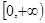 上是减函数
上是减函数当
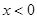 时,
时,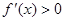 ,
,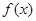 在区间
在区间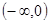 上是增函数---------------4分
上是增函数---------------4分(2)假设
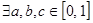 ,使得
,使得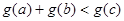 ,则
,则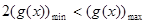 -----------5分
-----------5分由条件知:
 ,
,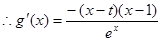 ------------------6分
------------------6分Ⅰ.当
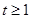 时,
时,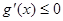 ,
,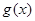 在
在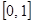 上单调递减,
上单调递减,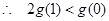 ,即
,即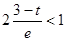 ,得:
,得: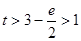 -----------7分
-----------7分Ⅱ.当
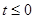 时,
时,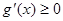 ,
,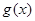 在
在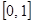 上单调递增
上单调递增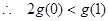 ,即
,即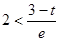 ,得:
,得: -----------8分
-----------8分Ⅲ.当
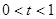 时
时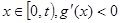 ,
,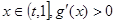 ,所以:
,所以: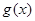 在
在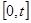 单调递减,在
单调递减,在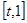 上单调递增
上单调递增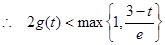 ,即
,即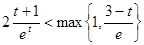 --------------------10分
--------------------10分由(1)知
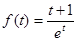 在
在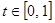 上单调递减,故有
上单调递减,故有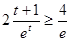
而
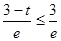 ,所以无解.
,所以无解.综上所述:存在
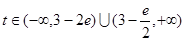 使得命题成立--------12分
使得命题成立--------12分
练习册系列答案
相关题目
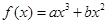 的图像经过点
的图像经过点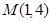 ,曲线在点
,曲线在点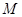 处的切线恰好与直线
处的切线恰好与直线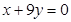 垂直.
垂直.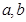 的值;
的值;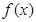 在区间
在区间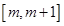 上单调递增,求实数
上单调递增,求实数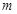 的取值范围.
的取值范围.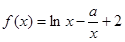 。
。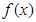 的单调区间;
的单调区间;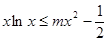 在
在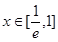 上恒成立,求
上恒成立,求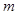 的取值范围。
的取值范围。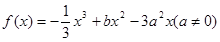 在
在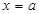 处取得极值.
处取得极值.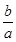 ;
;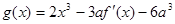 ,如果
,如果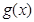 在开区间
在开区间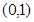 上存在极小值,求实数
上存在极小值,求实数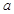 的取值范围.
的取值范围.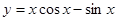 在下列哪个区间内是增函数( )
在下列哪个区间内是增函数( )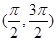
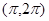
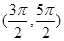
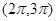
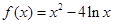 ,
,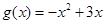 ;
;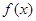 在
在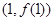 处的切线方程;
处的切线方程;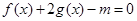 有唯一解,求
有唯一解,求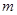 的取值范围;
的取值范围;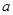 ,使得
,使得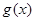 在
在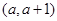 上均为增函数,若存在求出
上均为增函数,若存在求出