题目内容
【题目】在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
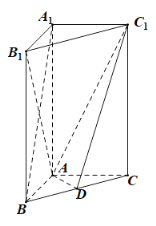
(1)求异面直线![]() ,
,![]() 所成角的余弦值;
所成角的余弦值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求异面直线![]() 与
与![]() 的距离.
的距离.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]()
【解析】
根据已知条件以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立按直角坐标系
轴建立按直角坐标系![]() ,写出相关点的坐标,(1)由各个点的坐标写出相应向量
,写出相关点的坐标,(1)由各个点的坐标写出相应向量![]() ,
,![]() ,代入向量夹角公式,即可求出异面直线
,代入向量夹角公式,即可求出异面直线![]() ,
,![]() 所成角的余弦值;
所成角的余弦值;
(2)先设平面![]() 的法向量为
的法向量为![]() 并求出法向量为
并求出法向量为![]() ,再利用直线
,再利用直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 的正弦值
的正弦值![]() 即可求出;
即可求出;
(3) 连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,可得
,可得![]() ,即
,即![]() 平面
平面![]() ,所以异面直线
,所以异面直线![]() 与
与![]() 的距离可转化为点
的距离可转化为点![]() 到平面
到平面![]() 的距离,根据点到平面的距离公式
的距离,根据点到平面的距离公式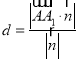 即可求出距离.
即可求出距离.
解:以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立按直角坐标系
轴建立按直角坐标系![]() ,
,
则各点的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .如图:
.如图:
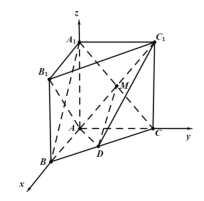
(1)所以![]() ,
,![]() ,
,
所以![]() .
.
故异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(2)![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() .
.
则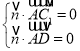 即
即![]() ,取
,取![]() ,得
,得![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则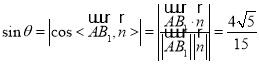 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,易得
,易得![]() ,
,
所以![]() 平面
平面![]() ,故点
,故点![]() 到平面
到平面![]() 的距离即为所求异面直线距离.
的距离即为所求异面直线距离.
记点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则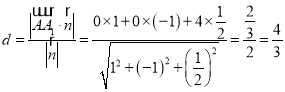 .
.
所以异面直线![]() 与
与![]() 的距离为
的距离为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】据统计,某5家鲜花店今年4月的销售额和利润额资料如下表:
鲜花店名称 | A | B | C | D | E |
销售额x(千元) | 3 | 5 | 6 | 7 | 9 |
利润额y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法计算利润额y关于销售额x的回归直线方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鲜花店的销售额为8千元时,利用(1)的结论估计这家鲜花店的利润额是多少.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计值公式分别为
中斜率和截距的最小二乘法估计值公式分别为