题目内容
8.从1,2,4,8这4个数中一次随机地取两个数,则所取两个数的乘积为8的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 首先列举并求出“从1,2,4,8这4个数中一次随机抽取2个数”的基本事件的个数再从中找到满足“所取2个数的乘积为8”的事件的个数,利用概率公式计算即可.
解答 解:从1,2,4,8这4个数中一次随机抽取2个数的所有基本事件有(1,2),(1,4),(1,8),(2,4),(2,8),(4,8)共6个,
所取2个数的乘积为8的基本事件有(1,8),(2,4)共2个,
故所求概率P=$\frac{2}{6}$=$\frac{1}{3}$.
故选:C.
点评 本题主要考查了古典概型的概率公式的应用,关键是一一列举出所有的基本事件.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
19.已知复数z=$\frac{a+4i}{1+ai}$,a>0,且z=$\overline{z}$,若1+ai是关于x的方程x2+bx+c=0的一根,则b,c分别为( )
| A. | 4,-8 | B. | 2,-5 | C. | -4,8 | D. | -2,5 |
3.4名优秀学生全部保送到3所学校去,每所学校至少去一名学生,则不同的保送方案有( )
| A. | 12种 | B. | 72种 | C. | 18种 | D. | 36种 |
13.计算22+42+62+…+1002的算法的程序框图是( )
| A. | 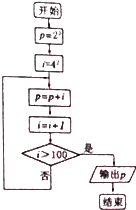 | B. | 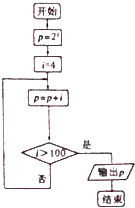 | C. | 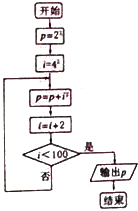 | D. | 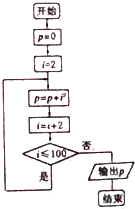 |
18.为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下资料:
(Ⅰ)从这5天中任选2天,记发芽的种子数分别为m,n,求事件“m,n均不小于25”的概率.
(Ⅱ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{b}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(Ⅱ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{b}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)