Question

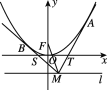
【题目】如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA的延长线上．

（1）若 = ， =1，求 的值；
（2）若EF2=FAFB，证明：EF∥CD．

Answer 1

【答案】
（1）解：∵A，B，C，D四点共圆，

∴∠ECD=∠EAB，∠EDC=∠B

∴△EDC∽△EBA，可得 = = ，

∴ =（ ）2，即 =（ ）2

∴ =

（2）解：证明：∵EF2=FAFB，

∴ = ，

又∵∠EFA=∠BFE，

∴△FAE∽△FEB，可得∠FEA=∠EBF，

又∵A，B，C，D四点共圆，

∴∠EDC=∠EBF，

∴∠FEA=∠EDC，

∴EF∥CD．

【解析】（1）根据圆内接四边形的性质，可得∠ECD=∠EAB，∠EDC=∠B，从而△EDC∽△EBA，所以有 = = ，利用比例的性质可得 =（ ）2 ， 得到 = ；（2）根据题意中的比例中项，可得 = ，结合公共角可得△FAE∽△FEB，所以∠FEA=∠EBF，再由（I）的结论∠EDC=∠EBF，利用等量代换可得∠FEA=∠EDC，内错角相等，所以EF∥CD．