题目内容

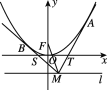
【题目】如图所示，以原点O为顶点，以y轴为对称轴的抛物线E的焦点为F(0，1)，点M是直线l：y＝m(m<0)上任意一点，过点M引抛物线E的两条切线分别交x轴于点S，T，切点分别为B，A.

(1)求抛物线E的方程；

(2)求证：点S，T在以FM为直径的圆上．

【答案】（1）；（2）见解析

【解析】

试题分析：第一问可以根据题意直接设出抛物线的标准方

程的形式，根据抛物线的焦点坐标，得出对应的的值，

从而得出抛物线的方程，第二问应用点在圆上的对应结论，即直径对的圆周角为直角，得出两线垂直的对应结果，从而得证，还有就是S，T两点证明的思路是一样的，所以，证明一个，另一个点可以用同理可得来带过.

试题解析：（Ⅰ）设抛物线E的方程为，

依题意，

所以抛物线E的方程为4分

（Ⅱ）设点

，否则切线不过点M

7分

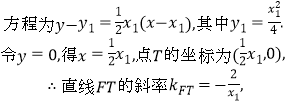
10分

∴AM⊥FT，即点T在以FM为直径的圆上；

同理可证点S在以FM为直径的圆上，

所以S，T在以FM为直径的圆上。 12分

练习册系列答案
相关题目

【题目】已知数列是公差为正数的等差数列，其前项和为，

且，

(1)求数列的通项公式．

(2)设数列满足，

①求数列的通项公式；

②是否存在正整数，使得，，成等差数列？若存在，求出的值；若不存在，请说明理由．

【题目】函数，函数 ，若对所有的总存在，使得成立，则实数的取值范围是__________．

【题目】已知函数f（x）= ，直线y= x为曲线y=f（x）的切线（e为自然对数的底数）．
（1）求实数a的值；
（2）用min{m，n}表示m，n中的最小值，设函数g（x）=min{f（x），x﹣ }（x＞0），若函数h（x）=g（x）﹣cx2为增函数，求实数c的取值范围．

【题目】已知命题p：x∈[－1，2]，函数f(x)＝x2－x的值大于0，若p∨q是真命题，则命题q可以是(　　)

A. x0∈(－1，1)，cos x0＜

B. “－3＜m＜0”是“函数f(x)＝x＋log2x＋m在区间上有零点”的必要不充分条件

C. x＝是曲线f(x)＝sin 2x＋cos 2x的一条对称轴

D. 若x∈(0，2)，则在曲线f(x)＝ex(x－2)上任意一点处的切线的斜率不小于

【题目】已知椭圆的离心率为，，分别为椭圆的左、右焦点，且.

（1）求椭圆的方程；

（2）设为椭圆上任意一点，以为圆心，为半径作圆，当圆与直线：有公共点时，求面积的最大值.

【题目】已知函数f（x）=lnx﹣a（x﹣1），g（x）=ex ．
（1）当a=2时，求函数f（x）的最值；
（2）当a≠0时，过原点分别作曲线y=f（x）与y=g（x）的切线l1 ， l2 ， 已知两切线的斜率互为倒数，证明： ＜a＜ ．

【题目】如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA的延长线上．

（1）若 = ， =1，求 的值；
（2）若EF2=FAFB，证明：EF∥CD．

【题目】某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

（1）求直方图中的值；

（2）求月平均用电量的众数和中位数；

（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网