题目内容
【题目】如图已知四棱锥P﹣ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E，F分别为棱BC，AD的中点．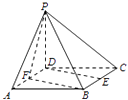 
（1）若PD=1，求异面直线PB和DE所成角的余弦值．
（2）若二面角P﹣BF﹣C的余弦值为 
，求四棱锥P﹣ABCD的体积．
【答案】
（1）证明：E，F分别为棱BC，AD的中点，ABCD是边长为2的正方形
∴DF∥BE且DF=BE
∴DFBE为平行四边形
∴DE∥BF
∴∠PBF是PB与DE的所成角
△PBF中，BF= 
，PF=， 
，PB=3，
∴cos∠PBF= 
，
∴异面直线PB和DE所成角的余弦值为 ；
（2）解：如图，以D为原点，射线DA，DC，DP分别为x，y，z轴建立空间直角坐标系．设PD=a，
可得如下点的坐标：
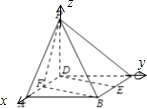
P（0，0，a），F（1，0，0），B（2，2，0）
则有： 
=（1，0，﹣a）， 
=（1，2，0）
因为PD⊥底面ABCD，所以平面ABCD的一个法向量为 
=（0，0，1）
设平面PFB的一个法向量为 
=（x，y，z），则可得 
，令x=1，得z= 
，y=﹣ 
，
所以 =（1，﹣ ， ）
由已知，二面角P﹣BF﹣C的余弦值为 
，所以得 
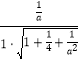= ，解得a=2．
因为PD是四棱锥P﹣ABCD的高，
所以其体积为VP﹣ABCD= 
×2×4= 
．
【解析】（1）根据一对对边平行且相等，得到一个四边形是平行四边形，根据平行四边形对边平行，把两条异面直线所成的角表示出来，放到△PBF中，利用余弦定理求出角的余弦值．（2）以D为原点，射线DA，DC，DP分别为x，y，z轴建立空间直角坐标系，设出线段的长，根据条件中所给的两个平面的二面角的值，求出设出的a的值，再求出四棱锥的体积．
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．
