题目内容
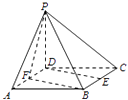
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() 分别为棱
分别为棱![]() 的中点.求证:
的中点.求证:
(1)![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
【答案】(1)详见解析; (2)详见解析.
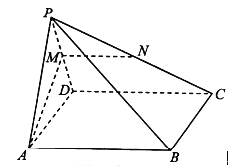
【解析】试题分析:(1)线面平行的证明则只需在面内找一线与之平行即可,因为M,N分别为棱PD,PC的中点,所以MN∥DC, 又因为底面ABCD是矩形,所以AB∥DC,
所以MN∥AB.(2)线面垂直则需要在面内找两根相交线与之垂直,因为AP=AD,M为PD的中点, 所以AM⊥PD.因为平面PAD⊥平面ABCD, 又平面PAD∩平面ABCD= AD,CD⊥AD,![]() 平面ABCD,所以CD⊥平面PAD. 又
平面ABCD,所以CD⊥平面PAD. 又![]() 平面PAD,所以CD⊥AM.
平面PAD,所以CD⊥AM.
试题解析:
(1)因为M,N分别为棱PD,PC的中点,所以MN∥DC, 又因为底面ABCD是矩形,所以AB∥DC,
所以MN∥AB. 又![]() 平面PAB,
平面PAB,![]() 平面PAB,所以MN∥平面PAB.
平面PAB,所以MN∥平面PAB.
(2)因为AP=AD,M为PD的中点, 所以AM⊥PD.因为平面PAD⊥平面ABCD, 又平面PAD∩平面ABCD= AD,CD⊥AD,![]() 平面ABCD,所以CD⊥平面PAD. 又
平面ABCD,所以CD⊥平面PAD. 又![]() 平面PAD,所以CD⊥AM. 因为CD,
平面PAD,所以CD⊥AM. 因为CD,![]() 平面PCD,
平面PCD,![]() ,所以AM⊥平面PCD.
,所以AM⊥平面PCD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目